Формула расчета процентов по кредиту

Учет дополнительных расходов

Если вы хотите посчитать переплату по кредиту максимально точно, то кроме суммы процентов, которые вы будете должны банку, стоит учесть все дополнительные расходы: на страховку, поездки в банк, штрафы за просрочку платежа, досрочное погашение и так далее.

Посчитать переплату с дополнительными расходами можно в кредитном калькуляторе, который учитывает комиссии. В поля для комиссии можно вписать любые траты: оплату проезда до банка, страховку, штрафы. Этот инструмент остался со времен, когда комиссии не были запрещены.

Дополнительные расходы увеличивают сумму переплаты по кредиту

Формы покрытия кредита

Такой серьёзный вопрос, как порядок возвращения заёмных средств, всегда оговаривается кредитно-финансовыми учреждениями заранее. Лишь после разъяснения всех нюансов клиенту кредит предоставляют в пользование.

Существует всего две формы погашения займа:

• дифференцированный платёж;
• аннуитетный платёж.

Большая часть заёмщиков по понятной причине в первую очередь обращает своё внимание на процентную ставку. Как правило, этот параметр является ключевым для среднестатистического обывателя, т.к

его воспринимают главным в вопросе определения объёма переплаты.

Однако также есть фактор способа начисления процентов и покрытия займа. Эти два обстоятельства оказывают не меньшее влияние на то, во сколько в итоге обойдётся кредит.

Примечание 1. Считается, что наиболее выгодной формой выплаты задолженности является дифференцированный платёж. В рамках данного способа погашения займа клиент банка покрывает сразу и тело кредита, и начисляемые проценты. За счёт этого каждый месяц выплаты сокращаются, т.к. проценты начисляются на постоянно уменьшающуюся сумму.

Выплата одновременно и самого долга, и процентной ставки, безусловно выгодна пользователю банковских услуг. Однако на практике сами кредитно-финансовые учреждения продвигают второй упомянутый нами способ покрытия кредита. Почему? Потому что они стремятся зарабатывать. Аннуитетный платёж подходит в этом случае лучше всего.

Это интересно: Работа кредитным специалистом — что нужно знать

Формула расчета

Тем не менее, в некоторых случаях вычисления вручную все-таки осуществляются. При этом используются следующие формулы:

• для аннуитетного платежа:
  • Платеж=Кредит*(Проц+(Проц/(1+Проц)*Мес-1)), где
    • Платеж – размер ежемесячной аннуитетной выплаты;
    • Кредит – сумма кредита;
    • Проц – величина процентной ставки;
    • Мес – срок действия кредита.
  • для дифференцированного платежа:
    • Платеж=Кредит/Мес + Остаток*Проц./12, где
      • Платеж – размер дифференцированного платежа;
      • Кредит – сумма кредита;
      • Мес – срок действия займа;
      • Остаток – задолженность по кредиту на момент начисления процентов;
      • Проц – величина процентной ставки.

Как рассчитать годовые проценты по кредиту?

Для аннуитетного платежа достаточно умножить сумму всего взятого кредита на процентную ставку. Наглядно это выглядит так:

10000 * 12% = 1200 рублей составит сумма, которую необходимо выплатить за пользование процентами банку.

При дифференцированном платеже сумма годовых процентов рассчитывается немого сложнее, поскольку необходимо помножить остаток по кредиту на процентную ставку и поделить на 12.

То есть, если из наших 10000 выплачено 5000, то: 5000 * 12%/12 = 50 рублей ежемесячно придется отдавать банку за пользование кредитом. При этом, помножив это же число на 12, получим среднюю сумму для оплаты процентов за весь год.

При обращении в банк для получения кредита следует уточнить, какая система кредитования работает в данной организации. Если предлагается сделать выбор самостоятельно, то есть смысл остановиться на дифференцированном платеже. По такому платежу меньше переплата, да и само осознание того, что платить приходится за свои деньги, является немаловажным фактором при выборе способа кредитования.

Ипотечные кредиты также выгодно выплачивать дифференцированно, так как при растущей стоимости недвижимости невыгодно выплачивать кредит с переплатой значительной суммы средств.

Самым оптимальным решением при выборе выплаты по кредиту будет попросить банковского служащего распечатать примерные графики и суммы платежей по обоим кредитам и сравнить, какой из них наиболее выгодный.

Также полезно будет узнать, какой вид платежа предлагается по умолчанию в каком-либо банке.

Использование офисных программ для работы со сложными процентами

Любой офисный пакет, а именно его табличный процессор, предоставляет множество функций для денежных расчетов: от самых простых и до самых сложных. Достаточно просто выбрать нужную (или несколько) для составления своих формул. Если использовать возможность программировать на VBA в Excel, то можно получать более быстрые результаты при расчетах. Когда рассчитывается сложная процентная ставка, формула может быть простейшей рекурсией без всяких степеней и логарифмов. Все сделает цикл с параметром в число периодов начисления. При необходимости можно легко добавить сумму периодического инвестирования, не ломая голову над выводом или поиском формул.

В примере, показанном ниже, используется, правда, не MS Excel, а LibreOffice Calc, – близнец Экселя для UNIX-подобных операционных систем. Но это, в принципе, ничего совершенно не меняет. Код макроса для OOBasic хоть и отличается от экселевского, но только в технических деталях.

В примере на рисунке выше мы рассчитываем как сложные, так и простые проценты по вкладу 8,6% годовых. Проценты начисляются каждый год, а вклад рассчитан на 18 лет вперед. Начальный взнос 25 тыс. рублей мы (условно) делаем 1 января 2017 года. Если мы хотим сравнить графики для этих результатов, что, конечно, более наглядно, то добро пожаловать на следующий лист, в который этот самый график очень легко вставить.

Пример показывает, что за прошедший срок составные проценты вдвое превышают простые.

Еще один пример. Можно легко переделать нашу модель и снять ограничение на ежегодную капитализацию. Тогда мы можем решить еще одну задачу. Предположим, что мы открыли центовый счет на бирже Forex и хотим поучаствовать в торговле валютами. Считая, что мы умеем, добросовестно работая с информацией, расти на 10% в день (что, может быть, слегка самонадеянно, но бог с ним), посмотрим, что получится из депозита в одну тысячу рублей, за месяц, т.е. 22 рабочих дня. Для этого чуть изменим формулу для нашего постоянного множителя:

Теперь мы избавились от (довольно искусственного) ограничения на ежегодный пересчет процентов. И получаем такую картину:

А на графике можем видеть рост и разницу между составными и обычными процентами:

И здесь видна разница между простыми и составными процентами.

Видео по теме

Немного о кредитном калькуляторе

Разбираться в банковских формулах по расчёту процентов по кредиту сможет не каждый. Поэтому вы можете посмотреть наш кредитный калькулятор. 

Это специальная программа, куда забиты уже все формулы. Нужны только ваши данные и команда к действию. 

Чтобы воспользоваться данным сервисом, стоит: 

1. Ввести в поля только цифры, без тире, точек, запятых;
2. Можно немного округлить, чтобы получилось лучше;
3. Потом кликнуть по надписи аннуитетный или дифференцированный платеж;
4. Затем нажать на «рассчитать».

Все. Программа покажет вам сумму переплат, итоговый процент переплаты и полную стоимость кредита. 

Калькуляторы есть и на почти всех банковских сайтах. Не забывайте ими пользоваться, когда рассматриваете, то или иное банковское предложение. 

Ключевые различия между простым интересом и сложным интересом

Ниже приведены основные различия между простым и сложным интересом:

1. Проценты, начисляемые на основную сумму за весь срок кредита, известны как простые проценты. Проценты, начисляемые как на основную сумму, так и на ранее заработанные проценты, называются сложными процентами.
2. Сложный процент дает высокую доходность по сравнению с простым процентом.
3. В Простом Проценте основное значение остается постоянным, в то время как в случае Сложного Процента Основное значение изменяется из-за эффекта сложения.
4. Темпы роста Простых процентов ниже, чем сложных процентов.
5. Расчет простого процента прост, а расчет сложного процента сложен.

пример

Предположим, Алекс депонировал рупий. 1000 в банк под 5% годовых (простой и составной) в год на 3 года. Узнайте общий интерес, который он получит в конце третьего года?

Решение : здесь P = 1000, r = 5% и t = 3 года

Простой интерес =

Сложный процент =

Заключение

Проценты — это плата за использование чужих денег. Существует много причин для выплаты процентов, таких как временная стоимость денег, инфляция, альтернативные издержки и фактор риска. Простой процент быстро рассчитывается, но сложный процент практически сложен. Если вы рассчитываете как простой процент, так и сложный процент для данного принципала, ставки и времени, вы всегда обнаружите, что сложный процент всегда выше, чем простой процент из-за сложного эффекта на него.

Понятие простых процентов и как они рассчитываются

Простые проценты – это проценты, начисляющиеся лишь на первоначальную величину вклада, независимо от количества периодов и их продолжительности. Они считаются один раз по окончанию срока депозита. Это обозначает, что сумма процентов за предыдущий период не учитывается при расчете в следующем. 

Метод расчета простых процентов основан на принципе наращения денег по арифметической прогрессии. Допустим, инвестор в начале года положил в банк депозит на сумму 100 000 руб. под 10% годовых:

• через год он получит сумму, равную первоначально внесенным деньгам плюс начисленные проценты: 100 000 + 10 000 (чтобы высчитать процент нужно сумму вклада умножить на ставку и разделить на 100) = 110 000 (руб.);
• через 2 года сумма составит: 100 000 + (10 000 х 2) = 120 000 (руб.);
• через N лет вкладчик получит: 100 000 + (10 000 х N).

Поскольку банки указывают ставку за год, то чтобы определить доход за другой период (к примеру, 3 месяца), применяя простую ставку процентов, формула будет такой:

S = (P x I x Т / K) / 100, где:

S– сумма насчитанных процентов (руб.);

P– начальная сумма вложенных средств;

I– процентная ставка за год;

Т – срок действия вклада в днях;

K– число дней в году.

То есть при вкладе 100 000 руб. на 3 месяца под 10% годовыхвычисление простых процентовбудет выполняться так:

(100 000 х 10 х 92 / 365) / 100 = 2520,55 (руб.).

Получается, что в конце срока вкладчик получит на руки внесенные 100 000 руб. плюс 2520,55 руб. дохода, т.е. 102 520,55 руб.

Это интересно: Обязанности таможенного брокера, кто это такой

Платежи и проценты по кредиту

Тип платежа соискатель выбирает сам, исходя из периодичности и размера личных финансовых поступлений. Аннуитетные и дифференцированные выплаты имеют существенные отличия, которые определяют их достоинства и недостатки.

Аннуитетный

Клиент совершает фиксированные ежемесячные взносы, первая часть которых идёт на погашение процентов по договору, вторая – уменьшает тело кредита. Проценты начисляются на фактическую сумму долга, а она с каждым периодом уменьшается, в последующих выплатах соотношение частей будет изменяться. При этом сумма основного платежа останется неизменной.

Кредитный калькулятор при выборе аннуитета по заданным соискателем параметрам рассчитывает:

1. Процентную ставку за платёжный период, чаще всего это 1 месяц (ПСМ). Вычисляется следующим образом: ПСГ/100/12 (количество месяцев в году).

1. Коэффициент аннуитета (КА) по формуле, где * — степень, равная общему количеству платежей:

ПСМ x (1 + ПСМ) *

(1 + ПСМ) * — 1

1. Сумму аннуитетного платежа (АП), которая равна: ОД x КА.

1. Проценты (СП) по формуле, где СЗ – размер фактической задолженности, которая в первом взносе всегда равна ОД: СЗ x ПСМ.

1. Их долю (ДСП): АП – СП.

1. Долю погашения ОД (ДОД): АП – ДСП.

Анализ расчётов, диаграммы и графика онлайн-сервиса Сбербанка покажет, что аннуитетный тип наиболее выгоден для финансового учреждения (переплата выше, чем при дифференцированном). Но он удобен для клиентов, которые получают стабильный фиксированный доход.

 Дифференцированный

На практике данный тип платежей применяется для ипотечных кредитов, но нередко банки используют его для потребительских программ. Главное отличие – стабильное уменьшение суммы ежемесячного платежа на протяжении всего срока действия договора. Основная финансовая нагрузка приходится на первые месяцы. Доля погашения ОД остаётся фиксированной для каждого периода, а размер процентов уменьшается.

Алгоритм расчёта параметров кредита с дифференцированным типом выплат для онлайн-калькулятора выглядит проще и состоит из вычислений:

1. Доли платежей, ежемесячно погашающих ОД – соотношение ОД и количества периодов срока кредитования (количество месяцев).
2. Доли процентов: произведение фактического ОД на ПСМ.
3. Размер дифференцированного платежа (ДП) для каждого периода: сумма доли процентов и ОД.

Проценты так же начисляются на остаток ОД, то есть их сумма становится меньше с каждым периодом.

Анализ результатов кредитного калькулятора покажет, что при строгом соблюдении графика выплат, дифференцированный тип предпочтительнее для некоторых клиентов, так как уменьшает переплату по продукту.

С помощью формул, соискатель может провести все расчёты по кредиту самостоятельно, но проще доверить эту работу кредитному калькулятору.

Что влияет на размер ставки по кредиту?

Банки, рекламируя свои услуги, чаще всего указывают минимальную ставку процента. Однако не стоит сразу бежать оформлять кредит, если по телевизору замелькала фраза: «кредит от 8%»

Ведь самое важно здесь «ОТ». На величину ставки влияет множество факторов:

• ставка будет меньше, если сумма займа — больше;
• чем дольше срок кредитования, тем ниже проценты;
• рассчитывать на меньшую ставку сможет тот, кто является зарплатным клиентом банка в котором планируется оформление кредита;
• для сотрудников партнерских организаций банка тоже предусмотрены сниженные ставки процента;
• непосредственно влияет на величину ставки тип кредита (с поручителем, без обеспечения, с обеспечением), чем больше у банка гарантий, тем ниже ставка;
• наличие справки с подтвержденным доходом гарантирует более лояльное отношение банка, и как следствие более низкие проценты.

Факторы переплаты по кредиту

Кредитование может серьезно выручить человека в момент финансовых невзгод. Оно также является крепким подспорьем — с помощью заемных средств мы улучшаем качество жизни, покупая то, что раньше могли себе позволить лишь в далекой перспективе. Однако банки не предоставляют финансовый ресурс «просто так». В каждый кредит они включают переплату — сумму, которую заемщик платит сверх того, что им было получено в долг.

В итоге размер кредита разрастается и зависит от:

• Суммы основного долга;
• Срока кредитования;
• Процентной ставки;
• Схемы расчета;
• Дополнительных выплат (штрафов, комиссий).

Финучреждения кровно заинтересованы в переплате за кредит: чем выше прибыль от отдельного клиента, тем больше банк может реинвестировать в другой кредит, получая новые статьи дохода. Как же клиенту учесть все факторы и прикинуть стоимость ссуды?

Как рассчитать через Excel?

Рассчитать в Excel доход от депозита можно на примере. Если необходимо положить на депозит 50 000 руб. с процентной ставкой 8% на три года с ежемесячной капитализацией и просчитать размер дохода через 36 месяцев, нужно составить таблицу, в которую внести 5 столбиков:

1 – сверху вниз указываются месяцы от 1 до 36;

2 — (В4) вписывается в строку сумма вклада – 50 000 руб.;

3 – (С4) указывается % — 8;

4 – (D4) вставляется формула для расчета ежемесячных %: =B4*$C$4/12, в которой В4 – сумма вклада, С4 -% (нужно проставлять значок $, чтобы формула выбирала данное поле, или путем выделения графы С4 курсором с нажатием клавиши F4 на клавиатуре), 12 – месяцы (% высчитывается в годовых);

5 – (Е4) считается новая сумма вклада, которая будет использована для начисления процента. Нужно написать формулу =B4+D4, в которой В4 – сумма вклада, D4 – сумма %, которые были начислены. Это будет новая сумма вклада, исходя из которой начисляются %.

В графу В5 заносится формула = Е4, в которой Е4 – это сумма вклада на истекший месяц с процентами.

Далее нужно скопировать формулы:

• подвести курсор к углу ячейки В5, он изменится с белого плюса на черный;
• потянуть его вниз, произойдет автоматическое копирование формулы из этой ячейки в другие;
• эту же операцию нужно выполнить с формулами, вписанными в ячейки D4, E4.
• В итоге, если все выполнено правильно, должен получиться ответ 63 512 руб.

Пример сложного процента на банковском депозите

Удобно и выгодно, когда ваши деньги одномоментно задействованы в разных инструментах. Сразу рекомендую не только у менеджера устно, но и в письменном договоре детально изучить — какой именно процент используется и какие есть нюансы по нему. На некоторых банковских сайтах или в мобильных приложениях есть калькулятор сложных процентов с капитализацией и пополнением. Показываю, как работает эта формула.

1. Первоначальный вклад составил 100 тыс. рублей на 1 год с правом пополнения без ограничения суммы под 5% годовых.
2. Во втором полугодии вы добавили к вкладу еще 100 тыс. рублей.
3. За первую половину вы заработали (100000/100*5%) / 2=2500. Во втором полугодии получили (200000/100*5%) / 2 = 5000. Итого прибыль за год 7500.
4. Далее вы можете забрать свои 7500 или добавить их к 200 тыс. или увеличить вклад еще на определенную сумму.

Наиболее выгодно так работать с проверенными инструментами, поэтапно повышая сумму вклада и внося все данные в excel, чтобы не заблудиться.

 
Как правило, разница на доходе с правом неограниченного пополнения и на обычном способе не превышает 0,5-1% в год, а иногда и вовсе отсутствует.

Ради справедливости нужно рассмотреть и правило, как работает формула расчета простых процентов по кредиту, поскольку ее часто применяют в работе. Простой процент начисляется так: сумма кредита умножается на процентную ставку и поделенная на 365 дней. Для примера: у вас кредит на 100 тыс. рублей под 10% годовых. Если предложен дифференцированный способ, то ежемесячно вам будет начисляться 1000 рублей непосредственно за пользование средствами.

Оплачивая их, через определенный срок можно приступить к погашению самого «тела». Многие банки предлагают аннуитетный платеж, работающий по формуле сложного процента. Это означает, что вы будете оплачивать кредит плюс-минус равными долями. 1000 рублей в месяц за сам кредит и, например, 1000 рублей за само тело. Таким образом, уже на второй месяц проценты будут начисляться на 99 тыс. остатка и с каждым месяцем и платеж по процентам, и выплаты по кредиту будут уменьшаться.

Обратите внимание: сложные проценты по кредиту предлагаются на средних и высоких суммах, в частности, когда оформляете ипотеку или покупаете по договору автомобиль из салона. Хотя есть и аналогичные предложения среди кредитных карт, например, карта Халва, где выплаты подразумеваются равными долями за определенный период и иногда вовсе с минимальными процентами

Узнав способ начисления процента в рабочем инструменте, возможность вносить дополнительно средства или погашать кредит досрочно, важно обратить внимание еще на один аспект — ставку дисконтирования. Это величина, применяемая для пересчета грядущих денежных потоков в общую величину актуальной стоимости. С математической точки зрения, это формула, обратная сложному проценту

С ее помощью оценивается, сколько нужно сейчас инвестировать средств, чтобы, например, через 2 года, получить 100 тысяч. Рассчитывается она по формуле: итоговая сумма (100 тыс. руб) равно как произведение неизвестного на (1+0,1 (10% — средняя ставка банка)), возведенное в квадрат. Далее по правилу пропорции выделите тот самый Х (икс). Фактически, это 82644 рубля

С математической точки зрения, это формула, обратная сложному проценту. С ее помощью оценивается, сколько нужно сейчас инвестировать средств, чтобы, например, через 2 года, получить 100 тысяч. Рассчитывается она по формуле: итоговая сумма (100 тыс. руб) равно как произведение неизвестного на (1+0,1 (10% — средняя ставка банка)), возведенное в квадрат. Далее по правилу пропорции выделите тот самый Х (икс). Фактически, это 82644 рубля.

 
Учитывайте правило: ставка дисконтирования должна быть выше предложенной доходности.

В итоге подчеркну: сложные проценты в финансовых инструментах только на первый взгляд выглядят сложными, но, если разобраться в их сути, никаких камней преткновения не возникнет, а еще более — вы сможете получить существенную выгоду. Всем желаю только выгодных начислений для инвестиций и минимальных для кредита, если же вы все же решились его оформить.

Профессиональный инвестор с опытом работы 5 лет с разными финансовыми инструментами, ведет свой блог и консультирует вкладчиков. Собственные эффективные методики и информационное сопровождение инвестиций.

Расчёт доли тела кредита в аннуитетных платежах

Зная долю процентов в аннуитетном платеже, можно легко посчитать долю тела кредита. Формула расчёта проста и понятна:

Как видите, здесь нет ничего сложного. По сути, аннуитетный платёж содержит в себе две составляющие:

1. 1. Долю процентов по кредиту.
2. 2. Долю тела кредита.

Если нам известна величина самого аннуитетного платежа и размер процентной доли, то на погашение тела кредита в этом платеже пойдёт то, что останется после вычитания из него суммы процентов.

Расчёт доли тела кредита в нашем первом платеже выглядит так:

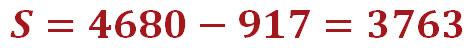
Надеемся, теперь всем понятно, откуда в графе «Погашение тела кредита» нашего графика аннуитетных платежей в выплатах за первый месяц взялась сумма 3763 руб. Да-да, это именно то, что осталось после того, как мы из суммы аннуитетного платежа (4680 руб.) вычли сумму процентов по кредиту (917 руб.). Аналогичным образом рассчитаны значения этой графы за последующие месяцы.

Итак, с телом кредита разобрались. Теперь осталось выяснить, как рассчитывается долг на конец месяца (в графике аннуитетных платежей это у нас последняя колонка).

Как рассчитать сложные проценты

Для того, чтобы просчитать, как приумножить деньги сложными процентами и какую прибыль принесет банковский вклад за несколько лет, нужно знать следующие показатели:

первоначальный размер вклада К0

ставка дохода R

количество лет, за которые нужно просчитать доход n

конечная сумма К

По следующей формуле можно рассчитать эту самую конечную прибыль: К=К0*(1+R)n А просчитав размер конечной суммы, легко можно установить размер прибыли – это разница между конечной и первоначальной суммами. При помощи приведенной выше формулы всегда можно просчитать, какой результат принесет в будущем инвестиция.

     Иногда возникают ситуации, когда нужно, наоборот, вычислить стартовую сумму вклада. Тогда эту формулу нужно преобразовать вот в такой вид: K0=K/(1+R)n С помощью формулы можно узнать и такой параметр, как процентная ставка. Эта информация требуется, когда инвестор, к примеру, хочет узнать, какую ставку ему выбрать, и на какой период нужно сделать вклад, чтобы получить конкретную прибыль. Формула вычисления сложных процентов: R=n?K/K0-1 А вот по этой формуле высчитывается период времени, на который нужно вложить средства, чтобы получить определенную желаемую прибыль: n=log1+R*K/K0

     При расчете срока вклада для получения определенной прибыли следует учитывать тот факт, что практически все банки используют целые периоды. То есть, если расчет по формуле показал, что средства для получения конкретной прибыли нужно вложить на 3 года и 9 месяцев, то нужно понимать, что в реальности необходимо будет положить депозит на 4 полных года. Есть и более сложные примеры расчетов прибыли по сложным процентам. К таким примерам относятся вклады с возможностью пополнения. Допустим, у вкладчика есть депозит, который он ежемесячно пополняет определенной суммой. Как же рассчитать, какую прибыль он получит с такого депозита?

Здесь уже простой формулой расчета не обойтись, нужны более сложные механизмы. Рассмотрим эту задачу на конкретном примере: вкладчик положил на счет 1000$ и каждый месяц добавляет к нему 50$. Допустим, процентная ставка составляет 1% в месяц. Для подсчета конечной суммы через пять лет нужно подставить в приведенные выше формулы показатели за каждый период, т.е. за 60 месяцев. Ведь сумма увеличивается не только за счет процентов, но и за счет ежемесячного добавления. При данных условиях по итогам первого месяца сумма на счету составила 1010$. К ней добавились еще 50$. То есть, для расчета конечной суммы во второй месяц процент нужно начислять уже на 1060$. И так далее, до окончания задуманного срока.

Конечно, каждый раз производить такие вычисления довольно сложно, особенно тем, кто не владеет достаточными познаниями в математике. Да и таблицы такие каждый раз не насоставляешься. Поэтому специально для вычисления сложных процентов по вкладам можно разработать свой калькулятор например в таблице excel.

Итак, очевидна разница между простыми и сложными процентами. Однако, следует отметить, что и схема простых процентов при грамотном ее использовании также может принести довольно хорошие результаты в виде прибыли. Более того, простые проценты являются единственным приемлемым вариантом, когда вкладчик нуждается в регулярном выводе средств со счета. Тогда он просто выводит сумму прибыли, накопившейся за месяц, полгода или год. Тогда как сложные проценты более приемлемы в случае долгосрочного вклада и повторного реинвестирования.

В каких случаях используется начисление простых и сложных процентов?

Формула простых процентов по вкладам применяется, когда полученные проценты плюсуются к телу депозита лишь в конце периода или совсем не прибавляются, а переводятся на другой счет. Формулу сложных процентов используют, когда проценты насчитываются через равные временные промежутки (месяц, квартал, год). Это означает проведение капитализации процентов (когда проценты насчитываются на проценты).

Простые проценты используются в случаях оформления краткосрочных вкладов, период действия которых, в основном, меньше года. Метод сложных процентов применяется при долгосрочных вкладах, которые открываются на срок больше года.

Штрафные санкции

Если клиент банка не выполняет свои долговые обязательства, финансовое учреждение имеет право начислить штраф. Условия обязательно должны быть описаны в договоре. Штраф может быть представлен как в виде фиксированной суммы, так и в форме процентной ставки. Если согласно договору штрафные санкции предусмотрены в размере 100 рублей, к примеру, сумму следующего минимального платежа будет рассчитать не трудно. Необходимо лишь прибавить 100 рублей.

https://www.youtube.com/watch?v=ytpolicyandsafetyru

500 : 100 х 5 = 25 рублей – сумма штрафа.

До 5 июня клиенту необходимо будет внести 1025 рублей (два минимальных платежа по 500 рублей и 25 рублей штрафа).

График платежей по кредиту (с применением формулы сложных процентов)

Исходные данные для расчёта полной стоимости кредита:

Сумма кредита 100 000 руб.

Проценты 36 % годовых

Срок кредитования 24 месяца

Комиссии 0 руб.

Составляем график по банковскому методу:

Период	Задолженность по кредиту, руб.	Аннуитетный платеж (ежемес. платеж), руб.	На проценты, 36 % х 30 / 365 = 2,959% = 0,02959	На погашение основного долга, руб.	Денежный поток  по-банковски (погашение «основного долга»), руб.
	З	А	П	О	ДП
	Зi = Зi-1 — О	const	П =  ДПi х 0,02959	О = А — П	ДПi = ДПi-1 — А + П                            или                                       ДПi = ДПi-1 — О
	100000,00				100000,00
1	97074,00	5885,00	2959,00	2926,00	97074,00
2	94061,42	5885,00	2872,42	3012,58	94061,42
3	90959,70	5885,00	2783,28	3101,72	90959,70
4	87766,19	5885,00	2691,50	3193,50	87766,19
5	84478,20	5885,00	2597,00	3288,00	84478,20
6	81092,91	5885,00	2499,71	3385,29	81092,91
7	77607,45	5885,00	2399,54	3485,46	77607,45
8	74018,85	5885,00	2296,40	3588,60	74018,85
9	70324,07	5885,00	2190,22	3694,78	70324,07
10	66519,96	5885,00	2080,89	3804,11	66519,96
11	62603,28	5885,00	1968,33	3916,67	62603,28
12	58570,71	5885,00	1852,43	4032,57	58570,71
13	54418,82	5885,00	1733,11	4151,89	54418,82
14	50144,07	5885,00	1610,25	4274,75	50144,07
15	45742,84	5885,00	1483,76	4401,24	45742,84
16	41211,37	5885,00	1353,53	4531,47	41211,37
17	36545,81	5885,00	1219,44	4665,56	36545,81
18	31742,20	5885,00	1081,39	4803,61	31742,20
19	26796,45	5885,00	939,25	4945,75	26796,45
20	21704,36	5885,00	792,91	5092,09	21704,36
21	16461,59	5885,00	642,23	5242,77	16461,59
22	11063,69	5885,00	487,10	5397,90	11063,69
23	5506,07	5885,00	327,37	5557,63	5506,07
24	0,00	5668,99	162,92	5506,07	0,00
Итог		141023,99	41023,99	100000,00

Сразу предлагаем вам сравнить этот график, рассчитанный по формуле сложных процентов, с графиком платежей того же самого кредита (на тех же условиях), но рассчитанным по формуле простых процентов:

2 графика платежей по одному кредиту-сложные и простые проценты

Рекомендуем не забыть прочитать след. статьи:

Вклад со сложным процентом

Рассматривая расчёт сложных процентов, подразумевают, что к депозиту после каждого периода начисления процентов (так называемого периода капитализации) прибавляется полученный доход.

Процент во втором периоде будет начислен на сумму плюс процент за первый период, в третьем периоде расчетная сумма уже увеличится, и процент тоже – он начисляется от суммы, увеличенной в результате прибавления двух разных процентов, причем второй будет выше первого.

Процент начисляется на процент, и каждый последующий период капитализации принесет доход выше, чем он был в прошлые периоды.

Длительность срока размещения денег при использования вклада с расчетом накоплений по формуле сложных процентов по вкладу играет ключевую роль. Чем дольше лежат деньги, тем выгоднее вклад.

Хитрость в том, что в линейке банковских вкладов вклады с капитализацией всегда предлагаются под более низкий процент, чем другие срочные вклады.

График погашения кредита, рассчитанного с применением формулы сложного процента зеркально отражает расчет процентов по вкладам с аналогичными условиями: чем больше срок кредита, тем интенсивнее растут проценты на его обслуживание.

Тонкости расчетов

Итак, формула кредита представляет собой простейшее математическое уравнение, в котором:

• Х – стоимость кредита;
• Х2 – полная стоимость кредита;
• Y- процентная ставка;
• R- сумма кредита;
• Z – срок кредитования.

Х=( R* Y)* Z

100%

А теперь приведем пример того, как рассчитать кредит самому:

Средняя процентная ставка по потребкредиту сегодня варьируется от 19 до 30%, возьмем за основу 25%.

Средняя запрашиваемая заемщиками сумма от 300 до 900 тысяч, возьмем для расчета – 500 тысяч.

Средний срок кредитования от 3-5 лет. Для понимания разницы, просчитаем оба срока.

Х = (500*25%)*3

100

Так, получаем Х= 125 тысяч (это стоимость 1 года кредитования или 25% годовых, или ¼ от суммы кредита).

Кредит мы будем платить 3 года, значит, Х= 125000*3 = 375 000

Полная стоимость кредита – это та сумма, которую клиент за 3 года должен вернуть банку или основной долг и проценты, считаем:

Х2 = 500 тыс. (основной долг) +375 тыс. (проценты)= 875 тыс.

Для 5 лет

Стоимость кредита составит – 125 тыс. * 5 = 625 тысяч

Полная стоимость кредита – 625 тыс. + 500 тыс. = 1125 000

В случае, если клиент берет кредит на 5 лет, сумма процентов превышает основной долг. Это нарушение закона, которое регулируется процентной ставкой. Таким образом, при долгосрочном кредите процентная ставка будет ниже, а при краткосрочном выше. В представленных расчетах была использована одинаковая процентная ставка.

Кроме того, выше представлен грубый расчет. Если будет рассчитывать банк, то он учтет, сколько клиент выплатит в счет основного долга за каждый год срока кредитования, то уменьшит стоимость кредита

Иными словами, за первый год платежей в сумму основного долга клиент внесет 100 тысяч, значит, в следующем году 25% годовых будет начислено не на 500, а на 400 тысяч,

За 2 год клиент внесет еще 200 тысяч, то процент буден начислен на 200 тысяч.