Как рассчитываются проценты по вкладам, и сколько банки готовы платить в 2021 году?

Расчет простых процентов за период в несколько месяцев

Формула простых процентов в этом случае будет иметь видP=P*(1+n/100*m/12)здесь обозначено m – количество месяцев (month).

Задача 3. Вкладчик разместил сумму размером 1600 рублей в банк на один год, однако ему пришлось забрать деньги через семь месяцев. Процентная ставка при досрочном снятии депозита составляет 9 % в год. Найти сумму, которую получит вкладчик.

Решение: Применяем формулу для вычислений

P=1600*(1+9/100*7/12)=1684 (рублей.) За 7 месяцев вкладчик получит 1684 рублей. Из приведенной формулы достаточно просто получить все необходимые величины для обратной задачи. Количество месяцев определяют по формулеm= (P/P-1)/n*100*12

а процентную ставку находят из зависимостиn= (P/P-1)/m*100*12

Капитализация процентов

На самом деле вклады под сложные проценты принято называть вклад с капитализацией процентов. Что это такое? Если говорить просто, то для вкладчика это означает начисление процентов на проценты. Например, по условиям банковского вклада прибыль от депозита начисляется ежемесячно, но, постольку, поскольку она остается не востребована вкладчиком, ее банк прибавляет к телу депозита.

Здесь размер прибыли во многом зависит от количества периодов капитализации. Многие крупные банки, в частности, Сбербанк России, ВТБ 24 и другие, предлагают своим клиентам капитализацию один раз в квартал, то есть каждые 3 месяца. А другие коммерческие банки могут вовсе рассчитывать прибыль один раз в год, соответственно, первая капитализация будет только через 12 месяцев, а именно на этот срок большинство заключает договор.

S=D×(1 N×L100×365)^x, где:

• S – общая сумма денежных средств, подлежащая возврату вкладчику по истечении срока действия депозитного договора;
• N – годовой процент без учета капитализации;
• L – число дней в том периоде, за который банк проводит капитализацию процентов;
• x – количество капитализаций за весь период действия договора;
• D – сумма инвестиций в банковский вклад.

Попробуем по данной формуле рассчитать депозит со следующими параметрами:

• сумма инвестиций — 10000 рублей;
• капитализация осуществляется один раз в месяц (всего в году 365 дней), соответственно здесь L будет равно 365/12=30,41;
• количество капитализации — 12;
• годовая ставка — 8%;

S=10000×(1 8×30,41100×365)^12= 10830 рублей – это общая прибыль по депозиту на конец срока действия договора.

Как видно, посчитать самостоятельно прибыль от депозита не так сложно. Но банки рассчитывают доход вкладчика с учетом капитализации процентов несколько по-другому. То есть, от базовой процентной ставки высчитывается эффективный процент по вкладу, то есть тот который будет действовать с учетом причисления процентов к телу депозита на протяжении срока действия депозитного договора.

((1 P/12)^x-1)×12/x, где:

• P – это годовой процент без учета капитализации;
• x – количество периодов капитализации (при том условии, если она осуществляется ежемесячно).

((1 8/100/12)^ 12-1)×12/12=0,083.

((1 P/100/4)^4-1)×100%.

Считаем вклад с теми же параметрами ((1 8/100/4)^4-1)×100%=0,2682417945625, или приблизительно 0,268.

При обычном вкладе начисленные проценты банк выплачивает вкладчику ежемесячно (либо с другой периодичностью, оговоренной условиями договора). Это называется «простые проценты». Вклад с капитализацией (или «сложные проценты») — это условие, при котором начисленные проценты не выплачиваются, а прибавляются к сумме вклада, таким образом увеличивая её. Общий доход от вклада в этом случае будет выше.

С помощью депозитного калькулятора вы можете сравнить результаты расчёта двух одинаковых вкладов (с капитализацией и без) и увидеть разницу.

Пример сложного процента на банковском депозите

Удобно и выгодно, когда ваши деньги одномоментно задействованы в разных инструментах. Сразу рекомендую не только у менеджера устно, но и в письменном договоре детально изучить — какой именно процент используется и какие есть нюансы по нему. На некоторых банковских сайтах или в мобильных приложениях есть калькулятор сложных процентов с капитализацией и пополнением. Показываю, как работает эта формула.

1. Первоначальный вклад составил 100 тыс. рублей на 1 год с правом пополнения без ограничения суммы под 5% годовых.
2. Во втором полугодии вы добавили к вкладу еще 100 тыс. рублей.
3. За первую половину вы заработали (100000/100*5%) / 2=2500. Во втором полугодии получили (200000/100*5%) / 2 = 5000. Итого прибыль за год 7500.
4. Далее вы можете забрать свои 7500 или добавить их к 200 тыс. или увеличить вклад еще на определенную сумму.

Наиболее выгодно так работать с проверенными инструментами, поэтапно повышая сумму вклада и внося все данные в excel, чтобы не заблудиться.

 
Как правило, разница на доходе с правом неограниченного пополнения и на обычном способе не превышает 0,5-1% в год, а иногда и вовсе отсутствует.

Ради справедливости нужно рассмотреть и правило, как работает формула расчета простых процентов по кредиту, поскольку ее часто применяют в работе. Простой процент начисляется так: сумма кредита умножается на процентную ставку и поделенная на 365 дней. Для примера: у вас кредит на 100 тыс. рублей под 10% годовых. Если предложен дифференцированный способ, то ежемесячно вам будет начисляться 1000 рублей непосредственно за пользование средствами.

Оплачивая их, через определенный срок можно приступить к погашению самого «тела». Многие банки предлагают аннуитетный платеж, работающий по формуле сложного процента. Это означает, что вы будете оплачивать кредит плюс-минус равными долями. 1000 рублей в месяц за сам кредит и, например, 1000 рублей за само тело. Таким образом, уже на второй месяц проценты будут начисляться на 99 тыс. остатка и с каждым месяцем и платеж по процентам, и выплаты по кредиту будут уменьшаться.

Обратите внимание: сложные проценты по кредиту предлагаются на средних и высоких суммах, в частности, когда оформляете ипотеку или покупаете по договору автомобиль из салона. Хотя есть и аналогичные предложения среди кредитных карт, например, карта Халва, где выплаты подразумеваются равными долями за определенный период и иногда вовсе с минимальными процентами

Узнав способ начисления процента в рабочем инструменте, возможность вносить дополнительно средства или погашать кредит досрочно, важно обратить внимание еще на один аспект — ставку дисконтирования. Это величина, применяемая для пересчета грядущих денежных потоков в общую величину актуальной стоимости. С математической точки зрения, это формула, обратная сложному проценту

С ее помощью оценивается, сколько нужно сейчас инвестировать средств, чтобы, например, через 2 года, получить 100 тысяч. Рассчитывается она по формуле: итоговая сумма (100 тыс. руб) равно как произведение неизвестного на (1+0,1 (10% — средняя ставка банка)), возведенное в квадрат. Далее по правилу пропорции выделите тот самый Х (икс). Фактически, это 82644 рубля

С математической точки зрения, это формула, обратная сложному проценту. С ее помощью оценивается, сколько нужно сейчас инвестировать средств, чтобы, например, через 2 года, получить 100 тысяч. Рассчитывается она по формуле: итоговая сумма (100 тыс. руб) равно как произведение неизвестного на (1+0,1 (10% — средняя ставка банка)), возведенное в квадрат. Далее по правилу пропорции выделите тот самый Х (икс). Фактически, это 82644 рубля.

 
Учитывайте правило: ставка дисконтирования должна быть выше предложенной доходности.

В итоге подчеркну: сложные проценты в финансовых инструментах только на первый взгляд выглядят сложными, но, если разобраться в их сути, никаких камней преткновения не возникнет, а еще более — вы сможете получить существенную выгоду. Всем желаю только выгодных начислений для инвестиций и минимальных для кредита, если же вы все же решились его оформить.

Профессиональный инвестор с опытом работы 5 лет с разными финансовыми инструментами, ведет свой блог и консультирует вкладчиков. Собственные эффективные методики и информационное сопровождение инвестиций.

Формула для расчета

Если рассчитать размер начисленных простых процентов достаточно легко (сумму инвестированных средств умножить на ставку на количество периодов начисления), то для расчета прибыли при капитализации потребуется использовать формулу посложнее:

Н=В*(1+%)^t, где

Н – размер начисления за весь период инвестирования;

В – сумма первоначальных вложений;

% — ставка;

t – количество периодов.

При этом нужно учитывать разницу между ежегодным начислением по ставке годовых и ежемесячным начислением по ставке из расчета в годовых.

В формуле расчета сложных процентов ставка выражается в долях, а не процентах (т.е. не 12%, а 0,12). При этом нужно учитывать в расчете периодичность начисления (ежегодно, ежемесячно, непрерывно).

Сравним:

1. Александр открыл депозит на 100 000 рублей под 12% годовых на 5 лет. Начисления происходят ежегодно и капитализируются.

Н=100 000*(1+0,12)^5= 176 234

Доход Александра составит через 5 лет: 176 234 – 100 000 = 76 234 рубля.

2. Александр открыл вклад на ту же сумму, срок и под 12%, но с ежемесячным начислением. Соответственно, каждый месяц сумма, начисленная за период, будет прибавляться к сумме инвестиций и порождать новый денежный поток.

Для расчета нам необходимо разделить годовую ставку на количество периодов начисления (т.е. на 12 месяцев), а количество периодов начисления наоборот, увеличить в 12 раз.

Н=100 000*(1+0,01)^60=181 669

Прибыль Александра составит 81 669 рублей. То есть через 5 лет депозит увеличится практически в 2 раза без дополнительных вложений со стороны инвестора.

Рассчитать доход при начислении чаще одного раза в год можно путем перевода годовой ставки по инвестиционному инструменту к ежемесячной. Это делается по формуле:

%=n*t/365(366), где

n — годовая ставка,

t – количество дней в периоде (при ежемесячном начислении – 30).

В нашем случае: %=0.12*30/365=0.01

Из этих примеров также видно, что чем чаще происходит капитализация, тем больший пассивный доход можно получить. При этом чем дольше срок инвестирования, тем разительнее отличается простой и сложный процент. При дополнительных вложениях размер начисляемых процентов со времени начинает превышать дополнительные взносы.

Например, если Александр начнет докладывать на депозит по 10 000 рублей в месяц, то размер процентов по окончании срока действия вклада составит 296 609 рублей, а общая сумма на конец 5 лет составит более 977 тысяч.

Гораздо реже используется формула непрерывного начисления процентов. При t стремящемся к бесконечности формула приобретает вид:

H=B*e^rt, где е~ 2,71828

Для расчета сложных процентов по депозиту в сети можно найти массу калькуляторов (например, на агрегаторе banki.ru) или же воспользоваться функцией БС (Будущая стоимость) в Excel.

Формула сложных процентов.

Она применяется реже в депозитной практике банка, но такие предложения найти можно. Для большинства вкладчиков они  не являются привлекательными по причине того, что ставки по ним ниже, чем по продуктам, когда доход начисляется  только по окончании действия депозитного договора. Периодичность присоединения дохода может быть разной: раз в месяц, раз в неделю, раз в квартал, каждый год. Она подразумевает под собой капитализацию или начисление «процентов на проценты».

Формула сложных %-ов:

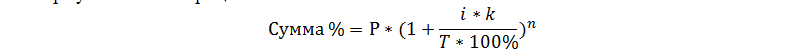
P – изначальная сумма вклада.

i – депозитная годовая ставка.

k – число дней в периоде, через который начисляется доход.

T – число дней в году.

n – число капитализаций дохода в течение всего срока депозита.

Рассмотрим пример №1: разместим 100 000 рублей под 12% годовых на полгода с ежемесячной капитализацией.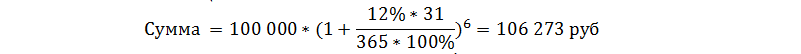
Полученное значение подтвердим через расчеты в Excel.

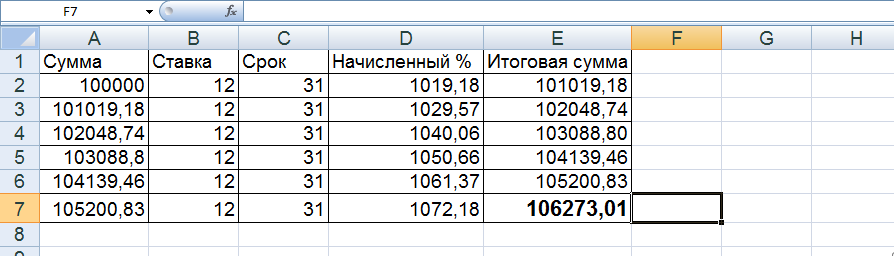
Таким образом, благодаря ежемесячной капитализации, общий итог вложений оказался выгоднее, чем в варианте, когда проценты причисляются  в конце срока.

Пример №2: разместим 100 000 рублей на 6 месяцев под 12% годовых с еженедельной капитализацией.

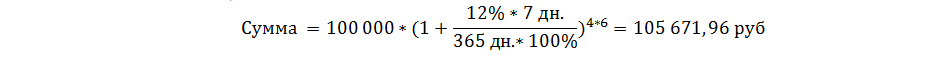
Полученное значение подтвердим через расчеты в Excel.

Пример №3: разместим 100 000 рублей на 1 год под 12% годовых с ежеквартальной капитализацией.

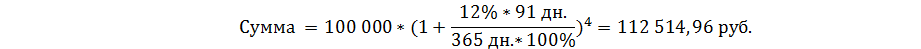
Полученное значение подтвердим через расчеты в Excel.

Пример №4: разместим 100 000 руб на 1 месяц под 12% годовых с ежедневной капитализацией.

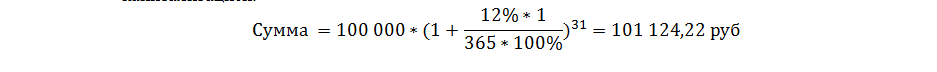
Полученное значение подтвердим через расчеты в Excel.

Таким образом, капитализация и формула сложных процентов дает более выгодный эффект, поэтому, при размещении денег в банке не стоит упускать из виду подобные варианты размещения.

Бесполезно
23

Занятно
20

Помогло
35

Расчет процентов по вкладу: формула

Если вы оформляете вклад с простыми процентами (без капитализации), то их легко можно рассчитать по следующей формуле.

Формула расчета процентов по вкладу:

S_п = (S_в*%*N_д)/N_г

где:

• S_п — сумма процентов по вкладу;
• S_в — сумма вклада;
• % — процентная ставка в виде десятичной дроби (например, при 15% годовых, %=0,15);
• N_д — число дней начисления процентов;
• N_г — число дней в году (365 или 366).

Для точного расчета процентов по вкладу нужно точно знать, сколько дней банк будет начислять вам проценты (это указывается в условиях договора). Например, дата зачисления средств может учитываться, а может не учитываться. Дата возврата средств, как правило, не учитывается.

Расчет процентов по вкладу с пополнением и/или снятием производится путем отдельного подсчета для каждого периода нахождения на депозите определенной суммы и суммирования этих результатов.

Рассмотрим, как работает формула расчета процентов по вкладу на примерах.

Как использовать сложные проценты в инвестировании

Как вы уже знаете, получаемая от инвестиций прибыль — это важный инструмент, который на большой дистанции может во много раз увеличить доходность ваших вложений. Метод повторного вложения прибыли называется реинвестированием.

Безусловно, использовать эффект сложного процента должен каждый инвестор, однако на практике это не так просто как кажется. Существует несколько проблем, которые мешают теоретически супервыгодное реинвестирование реализовать в реальных условиях. Например, вряд ли вы слышали о людях, ставших миллиардерами через банковские депозиты. Дело в том, что деньги постоянно обесцениваются из-за инфляции — постоянного повышения цен на товары и услуги. На самом деле ставка банковских депозитов обычно примерно равна инфляции или даже ниже, поэтому реальная доходность вкладов не впечатляет:

Скачать график в Excel

Даже если оставить удачный бескризисный отрезок 2010-2020 годов, доходность банковского вклада с учётом инфляции была в районе 1-2% годовых в рублях. Не говоря уже о доходности в долларах, которая после 2014 года, очевидно, находится в еще большем минусе.

Кроме инфляции сильно повлиять на итоговую доходность инвестиций могут разнообразные комиссии. Если их размер зависит от суммы инвестиций, убытки накапливаются по правилу сложных процентов, но уже с негативным эффектом. Это значит, что за несколько десятков лет инвестор может потерять сотни или даже тысячи процентов прибыли.

Такое часто встречается при инвестициях в ETF, где комиссия за управление достигает несколько процентов от депозита в год. Один из самых старых ETF под тикером SPY (инвестиционная стратегия — следование за индексом S&P 500) работает с 1993 года и берет с клиентов 0.09% в год — немного, по сравнению с другими биржевыми фондами. Эта ставка со временем может меняться, но давайте для эксперимента представим что она всегда была такой — и сравним, как будет отличаться доходность инвестиций при комиссиях от 0 до 2% в год:

Скачать график в Excel

Как видите, даже из-за несчастных 0.09% инвестор на дистанции 27 лет потерял 25% прибыли. А вроде бы небольшая комиссия в 2% годовых срезает доходность почти в 3 раза — с 723% до 270%, и это еще не учтена инфляция

По причине скрытых комиссий высокая доходность активов на самом деле может оказаться в разы ниже, поэтому перед принятием решения об инвестировании важно учитывать даже мизерные расходы

Куда же стоит инвестировать, чтобы использовать эффект сложного процента на максимум и минимизировать влияние инфляции и комиссий? Я бы выделил такие инструменты:

• Акции, в особенности американские. Сейчас это один из немногих активов, которые растут большую часть времени. Кроме того, многие компании платят дивиденды, которые можно реинвестировать и еще сильнее разгонять сложный процент. Плюс, рост цен на сами акции способен перекрыть влияние инфляции, а комиссии зависят от объема торгов, а не от вашего вклада. Взгляните на самых богатых людей планеты — почти все сделали состояние, владея большим количеством акций в своих компаниях.
• Инвестиционные фонды (в т.ч. ETF). Чаще всего это тоже инвестиции в акции, но вам не нужно самостоятельно подбирать портфель — аналитики фонда все сделают за вас. Если в портфеле фонда есть дивидендные акции, вы опять же сможете реинвестировать выплаты. При комиссии за участие ниже 1% в год катастрофического влияния на доходность ваших инвестиций не будет.
• Облигации. Обычно они дают чуть большую доходность, чем банковский депозит и способны практически без рисков приносить небольшую прибыль с учётом инфляции. В любом случае в вашем инвестиционном портфеле должны быть надёжные долгосрочные вложения, и облигации для этих целей подходят неплохо. Расходы при вложении в облигации идут на услуги фондового брокера и не зависят от общей суммы инвестиций.

Конечно, в любых инвестициях можно использовать правило сложных процентов, но не везде это рекомендуется делать. Чем выше риски вложений, тем выгоднее просто выводить прибыль, поскольку при неудачных раскладах депозит может быть потерян.

Использование сложных процентов — теоретически очень выгодное занятие, но как всегда дьявол кроется в деталях. Тем не менее, реинвестирование/капитализация остаётся одним из главных инструментов для накопления большого капитала, грех его игнорировать. И даже вне инвестирования начисление процентов по простому или сложному принципу встречается часто, поэтому полезно знать как это все работает. Надеюсь, подробный разбор формул и решения задач будут вам полезны.

Ну и подписывайтесь конечно 🙂

Удачных инвестиций и не болейте!

Проценты: правила

Рассмотрим четыре известных способа поиска процентов.

Занимайтесь математикой в удовольствие вместе с нашими преподавателями на курсах по математике для учеников с 1 по 11 классы!

Нахождение одного процента от числа

При делении на 100% получается 1% от этого числа. Это правило можно использовать по-разному. Например, чтобы узнать проценты от суммы, нужно умножить их на величину 1%. А чтобы перевести известное значение в проценты, следует разделить его на величину 1%. Этот метод отлично помогает в вопросе, как перевести целое число в проценты.

Представьте, что вы пришли в магазин за шоколадом. Обычно он стоит 250 рублей, но сегодня скидка 15%. Если у вас есть дисконтная карта магазина, шоколад обойдется вам в 225 рублей. Чем будет выгоднее воспользоваться: скидкой или картой?

Как решаем: Переведем 15% в рубли: 250 : 100 = 2,5 — это 1% от стоимости шоколада, значит, 2,5 × 15 = 37,5 — это 15%. 250 — 37,5 = 212,5. 212,5 < 225.

Ответ: выгоднее воспользоваться скидкой 15%.

Составление пропорции

Пропорция — определенное соотношение частей между собой. 

С помощью метода пропорции можно рассчитать любые проценты. Выглядит это так:

a : b = c : d. 

Читается: а относится к b так, как с относится к d

Также важно помнить, что произведение крайних членов равно произведению средних. Чтобы узнать неизвестное из этого равенства, нужно решить простейшее уравнение

Рассмотрим пример. Насколько выгодно покупать спортивную футболку за 1390 рублей при условии, что в магазине в честь дня всех влюбленных действует скидка 14%?

Как решаем: Найдем, сколько рублей составляет выгода, то есть скидка в 14%. Обозначим стоимость футболки за 100%, значит 1390 рублей = 100%. Тогда 14% это х рублей. Получаем пропорцию: 1390 руб. = 100% x руб. = 14% Перемножим крест-накрест и найдем x: x = 1390 × 14 : 100 x = 194,6

Ответ: выгода по скидке составила 194,6 рубля.

Соотношения чисел

Есть случаи, при которых можно использовать простые дроби. Например, 10% — это десятая часть целого. Чтобы найти 10% от числа a, нужно разделить его на 10. Собрали примеры соотношения чисел в таблице.

Процент	Дробь	Как найти % от числа a
10%	1/10	a : 10
20%	1/5	a : 5
25%	1/4	a : 4
50%	1/2	a : 2
75%	3/4	a : 4 × 3

Задача для тренировки. В черную пятницу вы нашли отличный пиджак со скидкой 25%. В обычный день он стоит 8500 рублей, но сейчас с собой есть только 6400 рублей. Хватит ли средств для покупки?

Как решаем: 100% — 25% = 75%, значит, нужно заплатить 75% от первоначальной цены. Используем правило соотношения чисел: 75% — это 3/4 от числа, значит, 8500 : 4 × 3 = 6375 (рублей).

Ответ: средств хватит, так как пиджак стоит 6375 рублей.

Обложение налогом

Налогом облагается любой доход гражданина РФ, установленный законодательством. В случае с банком таким доходом признается процент превышения ставки рефинансирования.

Ключевая ставка в 2019 году составляет 11%, а значит, если процент по депозиту выше этого значения, то на такой доход обязательно начисление налога на доходы физических лиц – 35%.

Если клиент разместит депозит на 10000 рублей сроком на 1 год под простой процент по ставке 12,3%, то по истечении срока договора должен будет уплатить в налоговую:

• 10000 *12,3% = 1230 рублей;
• 10000*11% = 1100 рублей;
• (1230-1100)*35% = 45,5 рублей.

Таким образом, в рассматриваемом примере видно, что налоги составят 45,5 рублей. Вычетом налогов занимается банк, а клиент просто получит на руки уменьшенную сумму.

Как работает сложный процент?

Сложный процент подразумевает использование начальной суммы и дохода, полученного во время предыдущих периодов. Таким примером может являться вклад в банке, в условиях которого указана капитализация полученной прибыли. Сумма процентов по вкладу, начисленная за первый месяц, добавляется к основному счёту, и во второй год процентная ставка применяется уже к увеличенной сумме, что обеспечивает рост итоговой прибыли.

Формула сложного процента

Расчёт будущей прибыли при использовании сложного процента производится по формуле:

, где:

– сумма, которую вы получите в конце периода;

– сумма первоначальных инвестиций, т.е. то, что вы вкладываете;

– годовая ставка;

– количество периодов начисления ставки (ежемесячно, ежеквартально, ежегодно и т.д.);

– общий срок вклада в годах.

Пример сложных процентов

Как мы выяснили выше, при использовании сложных процентов, прибыль по вкладу постоянно увеличивается. Сейчас посмотрим на примере, как это происходит.

Предположим, что у нас открыт вклад на сумму в 1000$ на 1 год со ставкой 5%. В этом случае, доход в конце года будет: 1000$ + 1000$ * (5 / 100) = 1050$. То есть мы просто посчитали простой процент для вклада на один год. Затем мы решили, что хотим снова открыть вклад ещё на 1 год. Тогда мы возьмём полученные ранее 1050$ и снова добавим их на вклад под 5% годовых. Тогда получится: 1050$ + 1050$ * (5 / 100) = 1102.5$.

Как видите, в первый год мы получили 1050$, а на второй год 1102$. Это и есть пример работы сложного процента, т.е. когда результат первого года (те самые 1050$), мы использовали для процента второго года и тем самым получили 1102$.

Если бы во второй год мы использовали простой процент, то мы брали не результат прошлого года (1050$), а взяли снова 1000$. И получилось бы:

• 1 год: 1050$
• 2 год: 1050$
• 3 год: 1050$
• 4 год: 1050$
• 5 год: 1050$

Спустя 5 лет, на вашем депозите будет 5250$. А вот как меняется ваш депозит, если используется сложный процент:

• 1 год: 1050$
• 2 год: 1102$
• 3 год: 1157$
• 4 год: 1215$
• 5 год: 1276$

То есть, спустя 5 лет, на вашем депозите будет 5800$. Как вы видите, разница существенна и именно в этом магия сложного процента. Чем дольше вы вкладываете деньги, используя прибыль, накопленную за предыдущие года – тем выше будет доход в конце.

Разница между простым и сложным процентами

Основная разница между двумя типами процента в том, на что именно начисляется процент. Когда используется простой, то за основу вычислений всегда берётся первоначальная сумма

Неважно, делаете вы расчёт для первого года или третьего – сумма всегда одна. Для сложного же процента – основа вычислений, это результат предыдущих вычислений

То есть то, что вы рассчитывали для прошлого года, берётся за основу расчётов для текущего года. Кратко: простой процент – основа всегда одинакова, сложный процент – основа всегда разная.

Отличия между сложными и простыми процентами

Простой процент	Сложный процент
Доход начисляется один раз – в конце срока	Доход начисляется каждый год
При расчёте учитывается только начальная сумма	При расчёте учитывается начальная сумма плюс доход каждого года
Прибыль каждый год будет одинаковая.	Прибыль каждый год будет увеличиваться, то есть она всегда разная.

Простой расчет сложных процентов

Представим ситуацию — вы решили открыть депозит в банке, положив туда часть прибыли, что получили, занимаясь трейдингом на Санкт-Петербургской бирже самостоятельно или на доверительной основе через брокера. Самый простой способ расчета прибыли, полученной через сложные проценты в банковском депозите поэтапно, выглядит так:

1. Открыли вклад на 10 тысяч рублей под 5% годовых.
2. Через 365 дней прибыль составила 500 рублей.
3. Вы можете закрыть вклад, а можете его реинвестировать, добавив к нему 500 рублей прибыли и оформив договор на 10500.
4. Через год прибыль составит 525 рублей, а суммарно на счету будет 11025 р.

 
В банковской практике это принято называть капитализацией.

Формула расчета с начислением дохода 1 раз в год

Несмотря на то, что процент называют сложным, слишком сложного в нем нет ничего. Вложив в продукт, например, 100 долларов на 365 дней под 5% годовых с одноразовым начислением прибыли, на 366-ой день вы получите 105 долларов

Здесь нужно принимать во внимание еще одно правило банка — начисление процентов начинается на следующий день после открытия вклада, а вот кредит «работает» с дня заключения договора, то есть непосредственно с сегодня

Зависимость от сроков

Конечный доход от вклада зависит от сроков и рассчитать его вручную достаточно просто.

При вкладе на 10000 рублей под ставку 8% годовых расчет произведем следующим образом:

• определим, чему равно каждодневное начисление 1%: 10000/100 = 100 рублей;
• умножим на количество процентов, которые дает банк: 100*8 = 800 рублей;
• прибавим процент к телу вклада: 10000 800 = 10800 рублей.

Если деньги размещаются не на год, а на другой срок, то процент рассчитать сложнее. Рассмотрим на том же примере, но срок вклада составит 182 дня.

В банках сроки вкладов указываются в месяцах или годах, но в расчете все равно используются дни.

Так, частыми сроками являются:

• 1 месяц – 30 дней;
• 3 месяца – 90 дней;
• полгода – 182 дня;
• год – 365 дней.

Например, 20 февраля клиент открывает депозит с ежеквартальной капитализацией. Сумма вклада 10000 рублей, ставка 10%. Срок – 9 месяцев или 272 дня. 15 августа снял 5000 рублей.

Дни	Дата	Приход	Расход	Сумма на счёте
	20 февраля 2019	10000		5000
49	10 апреля 2019	30000		35000
42	20 мая 2019	535		35535
85	15 августа 2019		5000	30535
6	20 августа 2019	744,77		31324,95
91	20 ноября 2019	789,95		32027,83

• С 20 февраля по 10 апреля: 10000*9/100*49/365 = 120,8.
• С 10 апреля по 20 мая: 40000*9/100*42/365 = 414,2.
• С 20 февраля по 20 мая: 120,8 414,2 = 535.
• С 20 мая по 15 августа: 35535 * 9/100 * 85/365 = 744,77.
• С 15 августа по 20 августа: 30535 * 9/100 * 6/365 = 45,18.
• С 20 мая по 20 августа: 744,77 45,18 = 789,95.
• С 20 августа по 20 ноября: 31324,95 * 9/100 * 91/365 = 702,88.

Ключевые различия между простым интересом и сложным интересом

Ниже приведены основные различия между простым и сложным интересом:

1. Проценты, начисляемые на основную сумму за весь срок кредита, известны как простые проценты. Проценты, начисляемые как на основную сумму, так и на ранее заработанные проценты, называются сложными процентами.
2. Сложный процент дает высокую доходность по сравнению с простым процентом.
3. В Простом Проценте основное значение остается постоянным, в то время как в случае Сложного Процента Основное значение изменяется из-за эффекта сложения.
4. Темпы роста Простых процентов ниже, чем сложных процентов.
5. Расчет простого процента прост, а расчет сложного процента сложен.

пример

Предположим, Алекс депонировал рупий. 1000 в банк под 5% годовых (простой и составной) в год на 3 года. Узнайте общий интерес, который он получит в конце третьего года?

Решение : здесь P = 1000, r = 5% и t = 3 года

Простой интерес =

Сложный процент =

Заключение

Проценты — это плата за использование чужих денег. Существует много причин для выплаты процентов, таких как временная стоимость денег, инфляция, альтернативные издержки и фактор риска. Простой процент быстро рассчитывается, но сложный процент практически сложен. Если вы рассчитываете как простой процент, так и сложный процент для данного принципала, ставки и времени, вы всегда обнаружите, что сложный процент всегда выше, чем простой процент из-за сложного эффекта на него.

Понятие простых процентов и как они рассчитываются

Простые проценты – это проценты, начисляющиеся лишь на первоначальную величину вклада, независимо от количества периодов и их продолжительности. Они считаются один раз по окончанию срока депозита. Это обозначает, что сумма процентов за предыдущий период не учитывается при расчете в следующем. 

Метод расчета простых процентов основан на принципе наращения денег по арифметической прогрессии. Допустим, инвестор в начале года положил в банк депозит на сумму 100 000 руб. под 10% годовых:

• через год он получит сумму, равную первоначально внесенным деньгам плюс начисленные проценты: 100 000 + 10 000 (чтобы высчитать процент нужно сумму вклада умножить на ставку и разделить на 100) = 110 000 (руб.);
• через 2 года сумма составит: 100 000 + (10 000 х 2) = 120 000 (руб.);
• через N лет вкладчик получит: 100 000 + (10 000 х N).

Поскольку банки указывают ставку за год, то чтобы определить доход за другой период (к примеру, 3 месяца), применяя простую ставку процентов, формула будет такой:

S = (P x I x Т / K) / 100, где:

S– сумма насчитанных процентов (руб.);

P– начальная сумма вложенных средств;

I– процентная ставка за год;

Т – срок действия вклада в днях;

K– число дней в году.

То есть при вкладе 100 000 руб. на 3 месяца под 10% годовыхвычисление простых процентовбудет выполняться так:

(100 000 х 10 х 92 / 365) / 100 = 2520,55 (руб.).

Получается, что в конце срока вкладчик получит на руки внесенные 100 000 руб. плюс 2520,55 руб. дохода, т.е. 102 520,55 руб.

Это интересно: Обязанности таможенного брокера, кто это такой

Расчет банковских процентов по вкладам — формула

Исходя из положений п. 1 ст. 838 Гражданского кодекса Российской Федерации (ГК РФ), формула расчета банковских процентов по вкладам зависит от того, как процент по вкладу определен в соглашении сторон.

Так, если процент прямо в договоре не установлен, то с учетом п. 1 ст. 809 ГК РФ он определяется на основании ставки банковского процента по месту нахождения вкладчика на дату выплаты денег. При этом особенности расчета процента могут иметь место в зависимости от того, открыт классический вклад или заведена сберегательная книжка, приобретен ли сберегательный сертификат.

Помимо собственно размера процента, для произведения расчета необходимо определить период, за который начисляются проценты, а также сумму, на которую они начисляются (включает она начисленные ранее проценты или ограничивается изначально внесенной суммой).

ВАЖНО! Согласно п. 1 ст. 839 ГК РФ день внесения банковского вклада для расчета процентов не учитывается, в то время как день выдачи денег включается в расчет.

В соответствии с п. 2 указанной статьи проценты выплачиваются ежеквартально или входят в общую сумму для расчета последующих процентов, если не были востребованы вкладчиком. Иной порядок может быть определен соглашением сторон.

Что такое прогрессивное начисление по банковскому вкладу

Прогрессивное начисление как таковое используется в праве не только применительно к банковским вкладам.

Так, при взыскании денежных средств, присуждаемых за неисполнение судебного акта, в судебной практике, в частности, встречается такой подход, как установление прогрессивного начисления. Например, если за каждый последующий период неисполнения взыскивается сумма больше, чем предполагалась за неисполнение в менее продолжительные периоды просрочки (постановление 18-го арбитражного апелляционного суда от 26.06.2015 № 18АП-6587/2015 по делу № А07-4912/2014).

Применительно к банковским вкладам прогрессивное начисление может означать, например, отличие размера процентов в зависимости от суммы остатка на депозите (письмо Минфина РФ от 05.12.2011 № 03-04-06/6-332). Помимо роста ставки с ростом суммы на депозите, прогрессивное начисление процентов по вкладу может применяться в зависимости от срока вклада, например увеличение процентной ставки при превышении годичного срока вклада.

Прогрессивное начисление по банковскому вкладу как нарастание ставки в зависимости от времени, когда вклад востребуется вкладчиком, признается экспертами в качестве одного из механизмов, используемых банками для снижения рисков в своей профессиональной деятельности (п. 5 экспертного заключения по проекту Федерального закона «О внесении изменений в ст. 837 ГК РФ», принятого на заседании Совета при Президенте РФ по кодификации и совершенствованию гражданского законодательства 17.11.2003).