Ипотечный кредитный калькулятор в excel. как правильно рассчитать кредит в excel?

Расчет аннуитетных платежей по кредиту в Excel

За вычисление аннуитета в Excel отвечает функция ПЛТ. Принцип вычисления в общем виде заключается в выполнении следующих шагов:

1. Составить исходную таблицу данных.
2. Построить график погашения долга для каждого месяца.
3. Выделить первую ячейку в столбике «Платежи по кредиту» и ввести формулу расчета «ПЛТ ($В3/12;$В$4;$В$2)».
4. Получившееся значение растянуть для всех столбцов таблички.

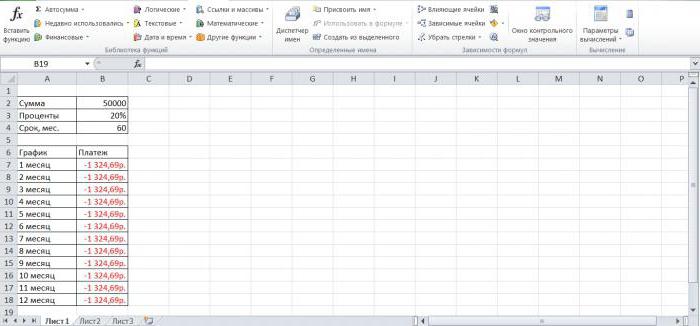Результат работы функции ПЛТ

Расчет в MS Excel погашение основной суммы долга

Аннуитетные платежи должны вноситься ежемесячно определенными суммами. Причем процентная ставка не изменяется.

Вычисление остатка суммы основного долга (при БС=0, тип=0)

Предположим, что кредит на 100000 рублей берется на 10 лет под 9%. Необходимо рассчитать сумму основного долга в 1 месяце 3-го года. Решение:

1. Составить таблицу данных и вычислить ежемесячный платеж по приведенной выше формуле ПС.
2. Рассчитать долю платежа, необходимую для погашения части долга, по формуле «=-ПМТ-(ПС-ПС1)*ставка=-ПМТ-(ПС +ПМТ+ПС*ставка)».
3. Посчитать сумму основного долга за 120 периодов по известной формуле.
4. Используя оператор ПРПЛТ найти количество процентов, выплаченных за 25 месяц.
5. Проверить результат.

Вычисление суммы основного долга, которая была выплачена в промежутке между двумя периодами

Такой расчет лучше сделать простым способом. Нужно использовать следующие формулы для вычисления суммы в промежутке за два периода:

• =«-БС(ставка; кон_период; плт; ; ) /(1+тип *ставка)».
• = «+ БС(ставка; нач_период-1; плт; ; ) /ЕСЛИ(нач_период =1;1; 1+тип *ставка)».

Досрочное погашение с уменьшением срока или выплаты

Если потребуется уменьшить срок кредитования, то придется производить дополнительные вычисления с помощью оператора ЕСЛИ. Так можно будет контролировать нулевой баланс, который не должен быть достигнут раньше окончания сроков выплаты.

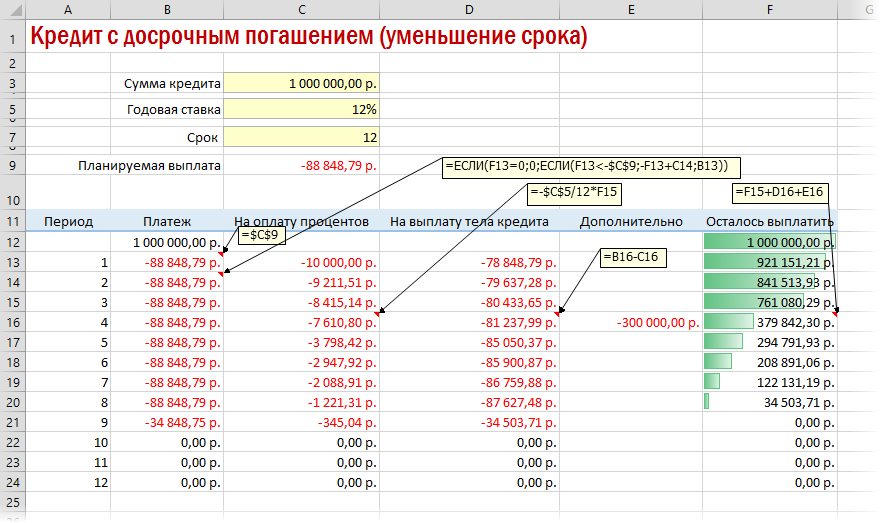Досрочное погашение с уменьшением срока

Чтобы снизить выплаты, нужно пересчитывать взнос за каждый предыдущий месяц.

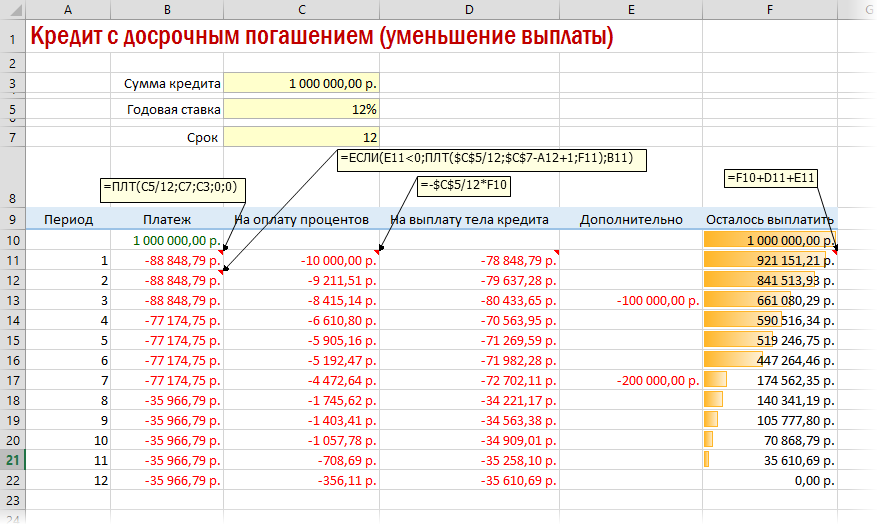Уменьшение выплат кредитования

Кредитный калькулятор с нерегулярными выплатами

Есть несколько вариантов аннуитета, когда заемщик может вносить нефиксированные суммы в любой день месяца. В такой ситуации остаток долга и проценты считаются за каждый день. При этом в Экселе надо:

1. Ввести числа месяца, по которым вносятся платежи, и указать их количество.
2. Проконтролировать отрицательные и положительные суммы. Отрицательные предпочтительнее.
3. Посчитать дни между двумя датами, в которые вносились деньги.

В Excel можно быстро посчитать размер регулярных выплат при условии, что уже накопилась фиксированная сумма. Данное действие выполняется с использованием функции ПЛТ после составления исходной таблицы.

Примеры расчетов регулярных платежей по аннуитетной схеме в Excel

Функция ОСПЛТ используется для расчетов задолженностей по аннуитетной схеме. То есть, сумма платежа за каждый период состоит из тела кредита (основной суммы задолженности) и процентов (части средств, которые выплачивают сверху за использование финансового продукта). Процентная ставка является неизменной величиной. Соотношение процентной части к телу кредита в каждом периодическом платеже меняется со временем. Рассматриваемая функция позволяет определить сумму основной задолженности (без учета процентов), выплаченной в определенный период согласно графику.

Пример 1. Банк выдал кредит на сумму 10 000 руб. под 18% годовых сроком на 1 год. Был составлен график ежемесячных выплат. Определить, какую сумму тела кредита выплатит клиент в 3-1 месяц.

Вид таблицы данных:

Для расчета используем следующую функцию:

=ОСПЛТ(B3/12;3;B4;B5)

Описание аргументов:

• B3/12 – размер ставки, приведенной к числу периодов выплат (12 месяцев);
• 3 – номер периода, для которого выполняется расчет;
• B4 – общее число периодов (12 месяцев в году);
• B5 – сумма кредита по договору.

Результат вычислений:

Полученное значение – отрицательное число, поскольку оно отражает расходы клиента по оплате финансового продукта.

Как рассчитать аннуитетный платеж в Excel

Те, кто читал предыдущую публикацию, наверняка ещё долго будут с ужасом вспоминать формулу аннуитетного платежа. Но сейчас вы, дорогие друзья, можете облегчённо вздохнуть, ибо все расчёты за вас сделает программа Microsoft Excel.

Мы сделаем не просто файлик с одной циферкой. Нет! Мы разработаем настоящий инструмент, с помощью которого вы сможете рассчитать аннуитетный платёж не только для себя, но и для соседа, который ставит свою машину на детской площадке; прыщавого студента, который сутками курит в вашем подъезде; тётки, которая выгуливает свою собаку прямо под вашими окнами – короче, для всех особо одарённых. Кстати, можете поставить где-нибудь возле монитора купюроприёмник и брать с этой публики деньги.

Давайте приступим к разработке нашего кредитного калькулятора. Смотрим на первый рисунок:

Итак, вы видите два блока. Один с исходными данными, а второй – с расчётами. Исходные данные (сумма кредита, годовая процентная ставка, срок кредитования) вы будете вводить вручную, а во втором блоке будут мгновенно появляться расчёты.

Начнём с расчёта ежемесячной суммы аннуитетного платежа. Для этого надо сделать активным окошко, в котором вы хотите видеть это значение (в нашем случае – это поле C11, на рисунке оно обведено и указано под номером 1). Далее слева от строки формул жмём на «fx» (на рисунке эта кнопка обведена и указана под номером 2). После этих действий у вас появится такая табличка:

Выбираем функцию «ПЛТ» и жмём «Ок». Перед вами появится таблица, в которую надо будет ввести исходные данные:

Здесь нам требуется заполнить три поля:

• «Ставка» – годовая процентная ставка по кредиту делённая на 12.
• «Кпер» – общий срок кредитования.
• «Пс» – сумма кредита (указывается со знаком минус).

Обратите внимание на то, что мы не вводим готовые цифры в эту таблицу, а указываем координаты ячеек нашего блока с исходными данными. Так, в поле «Ставка» мы указываем координаты ячейки, в которой будет вписываться вручную процентная ставка (C5) и делим её на 12; в поле «Кпер» указываются координаты ячейки, в которой будет вписываться срок кредитования (C6); в поле «Пс» – координаты ячейки в которой вписывается сумма кредита (C4). Так как сумма кредита у нас указывается со знаком минус, то перед координатой (C4) мы ставим знак минус

Так как сумма кредита у нас указывается со знаком минус, то перед координатой (C4) мы ставим знак минус.

После того как исходные данные будут введены, жмём кнопку «Ок». В результате мы видим в блоке расчетов точное значение ежемесячного аннуитетного платежа:

Итак, в данный момент сумма нашего аннуитетного платежа составляет 4680 руб (на рисунке он обведён и указан под номером 1). Если вы будете менять сумму кредита, процентную ставку и общий срок кредитования, то автоматически будет меняться значение вашего аннуитетного платежа.

Кстати, обратите внимание на значение функции, обозначенное на рисунке под номером 2: =ПЛТ(C5/12;C6;-C4). Да, да, это и есть те самые координаты, которые мы вводили в таблицу, выбрав функцию «ПЛТ». По сути, вы могли бы не проделывать всех тех сложных телодвижений, которые показаны на втором и третьем рисунках

Можно было просто вписать в строке формул то, что там сейчас вписано

По сути, вы могли бы не проделывать всех тех сложных телодвижений, которые показаны на втором и третьем рисунках. Можно было просто вписать в строке формул то, что там сейчас вписано.

Зная размер аннуитетного платежа несложно посчитать остальные значения нашего расчётного блока:

На рисунке наглядно показано, как рассчитана общая сумма выплат (обведена и указана под номером 1). Так как она равна сумме аннуитетного платежа (ячейка C11) умноженной на общее количество месяцев кредитования (ячейка C6), то мы и вписываем в строку формул следующую формулу: =C11*C6 (на рисунке она обведена и указана под номером 2). В результате мы получили значение 56 157 рублей.

Переплата по кредиту рассчитывается ещё проще. От общей суммы выплат (ячейка C12) надо отнять сумму кредита (ячейка C4). В строку вписываем такую формулу: =C12-C4. В нашем примере переплата равна: 6157 рублей.

Ну и последнее значение – эффективная процентная ставка (или полная стоимость кредита). Она рассчитывается так: общую сумму выплат (ячейка C12) делим на сумму кредита (ячейка C4), отнимаем единицу, затем делим всё это на срок кредитования в годах (ячейка C6 делённая на 12). В строке будет такая формула: =(C12/C4-1)/(C6/12). В нашем примере эффективная процентная ставка составляет 12,3%.

Всё! Вот таким нехитрым способом мы с вами составили в программе Microsoft Excel автоматический калькулятор расчета аннуитетных платежей по кредиту, скачать который можно ссылке ниже:

Калькулятор по кредиту с нерегулярными оплатами

Все больше становятся популярными те виды займов, в договоре которых прописан пункт о возможности внесения нерегулярных оплат. Это удобно – человек в любую, выбранную им дату, перечисляет определенную, доступную для него, сумму. Конечно, ставка при таком соглашении будет на порядок выше, но зато свобода действий заемщика – больше. Это позволит погасить долг в более короткие сроки, перекрыв, тем самым, переплату по процентам.

Для того чтобы рассчитать схему внесения средств и отследить, когда кредит будет полностью погашен, подойдет более развернутая модель калькулятора. В программе Эксель такой сервис имеется. Это расширенная таблица, содержащая дополнительные графы, позволяющие рассчитать взносы с точностью не до месяца, как в стандартной модели, а за каждый день. Принцип получения результата следующий:

• первые два столбца таблицы зеленого цвета – это дата и сумма внесения. После перечисления платежа и добавления его размера в строке, расположенной под ней, появится отрицательное число – это и будет остаточная величина долга;
• следующие два столбца – тело кредита и проценты. Прописанные в них формулы, позволят наглядно увидеть, какая долговая часть пойдет на погашения самого займа, а какая покроет проценты;
• последний, пятый столбец – общий долг к выплате. Для удобства пользователя он окрашен в желтый цвет.
• Расчет полной стоимости ссуды с помощью Эксель

Порядок определения полной суммы долга – исходя из тела ссуды и переплаты по процентам, регламентирован действующим законодательством о потребительском кредитовании населения. Согласно нормативному документу при проведении исчислений используется формула:

ПСК = i х ЧБП х 100, где

• i – переплата по процентной ставке за базовый срок;
• ЧПБ – количество таких сроков в одном календарном году.

Базовый период рассчитывается следующим образом. По закону, это стандартные временные рамки, чаще всего фигурирующие в типовых банковских графиках погашения задолженностей. Большинство отечественных финансовых учреждений применяют 28 дневный срок. Таким образом, базовый период равен 28. Следовательно, ЧПБ = 365 (количество дней в году) : 28. Получаем 13. Примечательно, что этот показатель так же, в большинстве случаев, стандартный.

Теперь, имея на руках все необходимые цифры, можно подставлять их в формулу. Например, клиент берет в долг 400 000 рублей, сроком на 2 года (24 месяца), под ставку 22% годовых.

Выходит:

ПСК = 22/13 х 13 х 100 = 22%

Получаем, что при отсутствии дополнительных или скрытых комиссионных начислений, нередко устанавливаемых банками, ПСК полностью совпала с величиной ставки.

Чтобы узнать, сколько же всего необходимо отдать компании, чтобы кредит считался закрытым, нужно к размеру взятых денежных средств прибавить ПСК – в нашем случае, это 22%.

В этом видео подробно рассказано о том, как правильно подсчитать проценты по кредиту в таблице Эксель:

Таким образом, становится понятно, что пользоваться кредитным калькулятором в программе Excel достаточно просто, а преимуществ – масса. Основное из них – достоверность полученных данных, тогда как многие банки грешат тем, что калькуляторы, которые они предлагают на своих сайтах, содержат заведомо скрытые комиссии. Они автоматически увеличивают общую переплату и величину текущих взносов.

Преимущества и недостатки аннуитетных платежей

Чтобы лучше разбираться в теме, необходимо изучить ключевые особенности данного типа кредитных платежей. Он имеет следующие преимущества:

• Установление конкретной суммы платежа и даты ее взноса.
• Высокая доступность для заемщиков. Практически любой человек сможет оформить аннуитет, независимо от своего финансового положения.
• Возможность понижения суммы ежемесячного взноса с повышением уровня инфляции.

Без недостатков не обошлось:

• Высокая ставка. Заемщик переплатит большую сумму денег по сравнению с дифференциальным платежом.
• Проблемы, возникающие при желании досрочно погасить долг.
• Отсутствие перерасчетов при досрочных выплатах.

Основная формула аннуитетного платежа в Excel

Как и говорилось выше, в Microsoft Office Excel можно работать с различными типами платежей по кредитам и ссудам. Аннуитет не является исключением. В общем виде формула, с помощью которой можно быстро вычислить аннуитетные взносы, выглядит следующим образом:  

Основные значения формулы расшифровываются так:

• АП – аннуитетный платеж (название сокращено).
• О – размер основного долга заемщика.
• ПС – процентная ставка, выдвигаемая ежемесячно конкретным банком.
• С – число месяцев, на протяжении которых длится кредитование.

Для усвоения информации достаточно привести несколько примеров использования данной формулы. О них пойдет речь далее.

Примеры использования функции ПЛТ в Excel

Приведем простое условие задачи. Необходимо посчитать ежемесячный кредитный платеж, если банк выдвигает процент в размере 23%, а общая сумма составляет 25000 рублей. Кредитование продлится на протяжении 3-х лет. Задача решается по алгоритму:

1. Составить общую таблицу в Excel по исходным данным.

Таблица, составленная по условию задачи. В действительности можно задействовать другие столбцы для ее размещения

1. Активировать функцию ПЛТ и ввести для нее аргументы в соответствующее окошко.
2. В поле «Ставка» прописать формулу «В3/В5». Это и будет процентная ставка по взятому кредиту.
3. В строке «Кпер» написать значение в виде «В4*В5». Это будет общее количество выплат за весь срок кредитования.
4. Заполнить поле «Пс». Здесь нужно указать первоначальную сумму, взятую в банке, прописав значение «В2».

Необходимые действия в окне «Аргументы функции». Здесь указан порядок заполнения каждого параметра

1. Удостовериться, что после нажать «ОК» в исходной таблице посчиталось значение «Ежемесячный платеж».

Финальный результат. Ежемесячный платёж посчитан и выделен красным цветом

Пример расчета суммы переплаты по кредиту в Excel

В этой задаче надо подсчитать сумму, которую переплатит человек, взявший кредит 50000 рублей по процентной ставке 27% на 5 лет. Всего в год заемщик производит 12 выплат. Решение:

1. Составить исходную таблицу данных.

Таблица, составленная по условию задачи

1. Из общей суммы выплат отнять первоначальный размер суммы по формуле «=ABS(ПЛТ(B3/B5;B4*B5;B2)*B4*B5)-B2». Ее надо вставить в строку формул сверху главного меню программы.
2. В итоге в последней строке созданной таблички появится сумма переплат. Заемщик переплатит 41606 рублей сверху.

Финальный результат. Практически двукратная переплата

Формула вычисления оптимального ежемесячного платежа по кредиту в Excel

Задача с таким условием: клиент зарегистрировал счет в банке на 200000 рублей с возможностью ежемесячного пополнения. Нужно посчитать количество платежа, который человек должен вносить каждый месяц, чтобы через 4 года на его счету оказалось 2000000 рублей. Ставка составляет 11%. Решение:

1. Составить табличку по исходным данным.

Таблица, составленная по данным из условия задачи

1. В строку ввода Эксель ввести формулу «=ПЛТ(B3/B5;B6*B5;-B2;B4)» и нажать «Enter» с клавиатуры. Буквы будут отличаться в зависимости от ячеек, в которых размещена таблица.
2. Проверить, что сумма взноса автоматически посчиталась в последней строке таблицы.

Окончательный результат расчета

Особенности использования функции ПЛТ в Excel

В общем виде данная формула записывается следующим образом: =ПЛТ(ставка; кпер; пс; ; ). У функции есть следующие особенности:

Когда рассчитываются ежемесячные взносы, в рассмотрение берется исключительно годовая ставка.
Указывая размер процентной ставки, важно сделать перерасчет, опираясь на число взносов за год.
Вместо аргумента «Кпер» в формуле указывается конкретное число. Это период выплат по задолженности.

График выплат

Сохранить в pdf Сохранить в Excel Распечатать Cсылка на расчет

Дата платежа	Остаток задолженности, руб.	Начисленные %, руб.	Платеж в основной долг, руб.	Сумма платежа, руб.
08.10.2018	310 000,00	3 821,92	3 552,96	7 374,88
08.11.2018	306 447,04	3 904,05	3 470,83	7 374,88
08.12.2018	302 976,21	3 735,32	3 639,56	7 374,88
08.01.2019	299 336,66	3 813,47	3 561,41	7 374,88
08.02.2019	295 775,25	3 768,10	3 606,78	7 374,88
08.03.2019	292 168,46	3 361,94	4 012,94	7 374,88
08.04.2019	288 155,52	3 671,02	3 703,86	7 374,88
08.05.2019	284 451,67	3 506,94	3 867,94	7 374,88
08.06.2019	280 583,73	3 574,56	3 800,32	7 374,88
08.07.2019	276 783,41	3 412,40	3 962,48	7 374,88
08.08.2019	272 820,93	3 475,66	3 899,21	7 374,88
08.09.2019	268 921,71	3 425,99	3 948,89	7 374,88
08.10.2019	264 972,83	3 266,79	4 108,09	7 374,88
08.11.2019	260 864,74	3 323,35	4 051,53	7 374,88
08.12.2019	256 813,20	3 166,19	4 208,69	7 374,88
08.01.2020	252 604,51	3 218,11	4 156,77	7 374,88
08.02.2020	248 447,75	3 165,16	4 209,72	7 374,88
08.03.2020	244 238,03	2 910,78	4 464,10	7 374,88
08.04.2020	239 773,93	3 054,65	4 320,22	7 374,88
08.05.2020	235 453,71	2 902,85	4 472,02	7 374,88
08.06.2020	230 981,68	2 942,64	4 432,23	7 374,88
08.07.2020	226 549,45	2 793,08	4 581,80	7 374,88
08.08.2020	221 967,64	2 827,81	4 547,07	7 374,88
08.09.2020	217 420,57	2 769,88	4 605,00	7 374,88
08.10.2020	212 815,57	2 623,75	4 751,12	7 374,88
08.11.2020	208 064,45	2 650,68	4 724,19	7 374,88
08.12.2020	203 340,25	2 506,93	4 867,94	7 374,88
08.01.2021	198 472,31	2 528,48	4 846,40	7 374,88
08.02.2021	193 625,91	2 466,74	4 908,14	7 374,88
08.03.2021	188 717,78	2 171,55	5 203,33	7 374,88
08.04.2021	183 514,44	2 337,92	5 036,95	7 374,88
08.05.2021	178 477,49	2 200,41	5 174,47	7 374,88
08.06.2021	173 303,02	2 207,83	5 167,05	7 374,88
08.07.2021	168 135,97	2 072,91	5 301,97	7 374,88
08.08.2021	162 834,00	2 074,46	5 300,42	7 374,88
08.09.2021	157 533,59	2 006,93	5 367,94	7 374,88
08.10.2021	152 165,64	1 876,01	5 498,86	7 374,88
08.11.2021	146 666,78	1 868,49	5 506,38	7 374,88
08.12.2021	141 160,40	1 740,33	5 634,54	7 374,88
08.01.2022	135 525,85	1 726,56	5 648,32	7 374,88
08.02.2022	129 877,54	1 654,60	5 720,27	7 374,88
08.03.2022	124 157,26	1 428,66	5 946,22	7 374,88
08.04.2022	118 211,04	1 505,98	5 868,90	7 374,88
08.05.2022	112 342,14	1 385,04	5 989,84	7 374,88
08.06.2022	106 352,30	1 354,90	6 019,98	7 374,88
08.07.2022	100 332,32	1 236,97	6 137,90	7 374,88
08.08.2022	94 194,42	1 200,01	6 174,87	7 374,88
08.09.2022	88 019,55	1 121,34	6 253,53	7 374,88
08.10.2022	81 766,02	1 008,07	6 366,80	7 374,88
08.11.2022	75 399,21	960,57	6 414,31	7 374,88
08.12.2022	68 984,90	850,50	6 524,38	7 374,88
08.01.2023	62 460,52	795,73	6 579,15	7 374,88
08.02.2023	55 881,37	711,91	6 662,96	7 374,88
08.03.2023	49 218,41	566,35	6 808,53	7 374,88
08.04.2023	42 409,88	540,29	6 834,59	7 374,88
08.05.2023	35 575,29	438,60	6 936,28	7 374,88
08.06.2023	28 639,01	364,85	7 010,03	7 374,88
08.07.2023	21 628,99	266,66	7 108,22	7 374,88
08.08.2023	14 520,77	184,99	7 189,89	7 374,88
08.09.2023	7 330,88	93,39	7 330,88	7 424,27

Показать все

Как рассчитать платежи по кредиту в Excel

Ежемесячные выплаты зависят от схемы погашения кредита. Различают аннуитетные и дифференцированные платежи:

1. Аннуитет предполагает, что клиент вносит каждый месяц одинаковую сумму.
2. При дифференцированной схеме погашения долга перед финансовой организацией проценты начисляются на остаток кредитной суммы. Поэтому ежемесячные платежи будут уменьшаться.

Чаще применяется аннуитет: выгоднее для банка и удобнее для большинства клиентов.

Расчет аннуитетных платежей по кредиту в Excel

Ежемесячная сумма аннуитетного платежа рассчитывается по формуле:

А = К * S

где:

• А – сумма платежа по кредиту;
• К – коэффициент аннуитетного платежа;
• S – величина займа.

Формула коэффициента аннуитета:

К = (i * (1 + i)^n) / ((1+i)^n-1)

• где i – процентная ставка за месяц, результат деления годовой ставки на 12;
• n – срок кредита в месяцах.

В программе Excel существует специальная функция, которая считает аннуитетные платежи. Это ПЛТ:

1. Заполним входные данные для расчета ежемесячных платежей по кредиту. Это сумма займа, проценты и срок.
2. Составим график погашения кредита. Пока пустой.
3. В первую ячейку столбца «Платежи по кредиту» вводиться формула расчета кредита аннуитетными платежами в Excel: =ПЛТ($B$3/12; $B$4; $B$2). Чтобы закрепить ячейки, используем абсолютные ссылки. Можно вводить в формулу непосредственно числа, а не ссылки на ячейки с данными. Тогда она примет следующий вид: =ПЛТ(18%/12; 36; 100000).

Ячейки окрасились в красный цвет, перед числами появился знак «минус», т.к. мы эти деньги будем отдавать банку, терять.

Расчет платежей в Excel по дифференцированной схеме погашения

Дифференцированный способ оплаты предполагает, что:

• сумма основного долга распределена по периодам выплат равными долями;
• проценты по кредиту начисляются на остаток.

Формула расчета дифференцированного платежа:

ДП = ОСЗ / (ПП + ОСЗ * ПС)

где:

• ДП – ежемесячный платеж по кредиту;
• ОСЗ – остаток займа;
• ПП – число оставшихся до конца срока погашения периодов;
• ПС – процентная ставка за месяц (годовую ставку делим на 12).

Составим график погашения предыдущего кредита по дифференцированной схеме.

Входные данные те же:

Составим график погашения займа:

Остаток задолженности по кредиту: в первый месяц равняется всей сумме: =$B$2. Во второй и последующие – рассчитывается по формуле: =ЕСЛИ(D10>$B$4;0;E9-G9). Где D10 – номер текущего периода, В4 – срок кредита; Е9 – остаток по кредиту в предыдущем периоде; G9 – сумма основного долга в предыдущем периоде.

Выплата процентов: остаток по кредиту в текущем периоде умножить на месячную процентную ставку, которая разделена на 12 месяцев: =E9*($B$3/12).

Выплата основного долга: сумму всего кредита разделить на срок: =ЕСЛИ(D9

Итоговый платеж: сумма «процентов» и «основного долга» в текущем периоде: =F8+G8.

Внесем формулы в соответствующие столбцы. Скопируем их на всю таблицу.

Сравним переплату при аннуитетной и дифференцированной схеме погашения кредита:

Красная цифра – аннуитет (брали 100 000 руб.), черная – дифференцированный способ.

Создание графика ссуды

Чтобы создать график ссуды, мы будем использовать различные формулы, описанные выше, и расширять их по количеству периодов.

В первом столбце периода введите «1» в качестве первого периода и затем перетащите ячейку вниз. В нашем случае нам нужно 120 периодов, так как 10-летний платеж по кредиту, умноженный на 12 месяцев, равен 120.

Второй столбец – это ежемесячная сумма, которую мы должны платить каждый месяц, которая является постоянной на протяжении всего графика кредита. Чтобы рассчитать сумму, вставьте следующую формулу в ячейку нашего первого периода:

= -PMT (TP; B4 * 12; B3) = -PMT ((1 + 3,10%) ^ (1/12) -1; 10 * 12; 120000)

Третий столбец – это основная сумма, которая будет выплачиваться ежемесячно. Например, за 40-й период мы выплатим 945,51 доллара в качестве основной суммы из нашей ежемесячной общей суммы в 1161,88 доллара.

Для расчета основной суммы выкупа мы используем следующую формулу:

= -PPMT (TP; A18; $ B $ 4 * 12; $ B $ 3) = -PPMT ((1 + 3,10%) ^ (1/12); 1; 10 * 12; 120000)

Четвертый столбец – это проценты, для которых мы используем формулу для расчета основной суммы, выплачиваемой с нашей ежемесячной суммы, чтобы определить, сколько процентов будет выплачено:

= -INTPER (TP; A18; $ B $ 4 * 12; $ B $ 3) = -INTPER ((1 + 3,10%) ^ (1/12); 1; 10 * 12; 120000)

В пятом столбце указана оставшаяся сумма оплаты. Например, после 40-го платежа нам придется заплатить 83 994,69 доллара на 120 000 долларов.

Формула выглядит следующим образом:

= $ B $ 3 + CUMPRINC (TP; $ B $ 4 * 12; $ B $ 3; 1; A18; 0)

В формуле используется комбинация основной суммы под периодом перед ячейкой, содержащей заимствованную основную сумму. Этот период начинает меняться, когда мы копируем и перетаскиваем ячейку вниз. В таблице ниже показано, что по истечении 120 периодов наша ссуда погашается.

Кредитный калькулятор в Excel по расчету графика аннуитетных платежей

Два предыдущих кредитных калькулятора очень удобны, но они выполняют краткие (общие) расчёты. А иногда заёмщику нужна расширенная информация — график ежемесячных аннуитетных платежей с детальной расшифровкой каждой выплаты (с указанием сумм, идущих на погашение процентов, и сумм, погашающих тело кредита). В общем, сейчас мы сделаем в программе Excel ещё один кредитный калькулятор, который будет автоматически рассчитывать график аннуитетных платежей. Щёлкаем мышкой по рисунку:

Перед вами расширенная и доработанная версия нашего первого кредитного калькулятора (того, который рассчитывает размер ежемесячного аннуитетного платежа по кредиту). Здесь кроме стандартных блоков с исходными данными и расчётами, появилась таблица, в которой детально расписаны все наши будущие ежемесячные выплаты. Таблица имеет пять колонок:

1. Месяцы. В этой колонке по порядку указаны номера месяцев, в которые будут осуществляться выплаты

Обратите внимание, что речь идёт не о календарных, а о порядковых номерах. То есть, если первая выплата припадает на сентябрь месяц, то ему присваивается порядковый номер «1», как первому месяцу, а не «9», как календарному.

2

Ежемесячный платёж. Это тот самый аннуитетный платёж, который не меняется на протяжении всего срока кредитования. В сноске к одной из ячеек вы можете увидеть данные, которые внесены в строку формул: =ПЛТ(B3/12;B4;-H14). Вы уже знаете, что за расчёт аннуитетного платежа в экселе отвечает функция ПЛТ. Координаты необходимых значений для расчёта можно внести, как через строку формул, так и заполнив таблицу, которая появится при нажатии на кнопку «fx», находящуюся слева от строки формул.

3. Погашение процентов. Здесь рассчитывается доля процентов в аннуитетных платежах (в каждой новой выплате она будет уменьшаться). В программе Excel за расчёт данного показателя отвечает функция ПРПЛТ. Опять же, задать необходимые параметры для расчётов можно либо нажав на кнопку «fx» и заполнив таблицу, либо просто внеся нужную информацию в строку формул. В нашем примере для расчёта доли процентов в первом платеже, в строке формул записано следующее: =ПРПЛТ(A15/12;D15;B15;-C15).

4. Погашение тела кредита. Та самая выплата, которая вытягивает нас из долговой ямы и избавляет от банковского рабства. Мы рассчитали её просто: из суммы аннуитетного платежа вычли долю процентов, которую рассчитали в предыдущей колонке. Собственно, в строке формул по первому платежу так и записано: =E15-F15. Но можно пойти и другим, более изощрённым, путём. В программе Excel за расчёт этого платежа отвечает функция ОСПЛТ. Можете для интереса нажать кнопку «fx», выбрать функцию ОСПЛТ, внести все необходимые данные и получить сумму, идущую на погашение тела кредита в выбранном платеже.

5. Долг на конец месяца. Ну, здесь всё просто! В данной колонке отображается сумма вашего долга перед банком на конец текущего месяца. Из текущего остатка мы отнимаем долю, идущую на погашение тела кредита. А вот уплаченные проценты просто уходят в казну банка и никак не влияют на сумму вашего текущего долга по кредиту.

Вот так легко и непринуждённо мы разработали кредитный калькулятор по расчёту графика аннуитетных платежей. Скачать его можно ссылке ниже:

Итак, друзья, теперь у вас есть целых три кредитных калькулятора по расчёту аннуитетных платежей, разработанных в программе Microsoft Excel. В следующей публикации мы расскажем о досрочном погашении аннуитетного кредита.

Кредитный калькулятор в Excel

Каждая финансовая компания, имеющая собственный сайт, предлагает пользователям опцию расчетов по кредитам. Воспользовавшись сервисом, потенциальный заемщик сможет наглядно увидеть размер своего текущего платежа, а так же общую сумму, которую он должен будет вернуть банку. Конечно, пользоваться таким программами легко и довольно удобно, однако желательно все же иметь собственного, домашнего помощника в подсчетах. Идеальный вариант – специальная программа, разработанная в Excel.

Данный сервис – это калькулятор, который даст возможность быстро посчитать различные виды выплат по кредитному соглашению, не требуя при этом прямого доступа к интернет-ресурсу. Человеку просто необходимо скачать приложение и выполнять математические подсчеты в любое удобное для него, время.

Обратите внимание! Программа достаточно популярна в бухгалтерском учете. Для того чтобы получить данные, потребуется минимум информации:

Для того чтобы получить данные, потребуется минимум информации:

• величина планируемого займа;
• целевое предназначение сделки;
• процентная ставка, действующая в банке на данный момент времени.

Программа выглядит в виде таблицы, поля которой заполняются данными. При работе с ней используются следующие функции:

• КПЕР – размер кредита в рублях;
• СТАВКА – величина переплаты. Измеряется в процентах на определенный промежуток времени. Чаще всего – за год;
• ПС – целевое предназначение займа;
• ПЛТ – текущий взнос по кредиту.

Если ввести в программу верхние три пункта, сервис в автоматическом режиме подсчитает последний, четвертый.

Справка! В программе так же есть опция составления персонального графика внесения денег на счет банка. Для этого дополнительно потребуется дата, с которой начал свое действие договор по займу. Она указывается в соглашении, подписанном сторонами.