Аннуитетные и дифференцированные платежи

Схема постнумерандо

А

Количество платежей	Количество начислений	S	A
p=1	m=1	R·(1+j)n−1j​	R·1−(1+j)−nj​
m>1	R·(1+jm​)m·n−1(1+jm​)m−1​	R·1−(1+jm​)−m·n(1+jm​)m−1​
p>1	m=1	Rp​·(1+j)n−1(1+j)1p​−1​	Rp​·1−(1+j)−n(1+j)1p​−1​
m=p	R·(1+jm​)m·n−1j​	R·1−(1+jm​)−m·nj​
m≠p	Rp​·(1+jm​)m·n−1(1+jm​)mp​−1​	Rp​·1−(1+jm​)−m·n(1+jm​)mp​−1​

Примеры задач по схеме постнумерандо

Решить

1. Определить современную стоимость и наращенную сумму аннуитета постнумерандо. Срок ренты n пять лет, разовый платеж R = 4000 руб. вносится ежегодно. На поступившие взносы начисляются проценты по сложной ставке j = 8% годовых.
   Платежи поступают в начале года (схема пренумерандо), периодичность взноса ренты p =1, проценты начсляются раз в год, m = 1.
   Будущая (наращенная) стоимость ренты: S=R·(1+j)n−1j​
   S=4 000·(1+0,08)5−10,08​ = 23 466,40 руб.
   Современная стоимость аннуитета: A=R·1−(1+j)−nj​
   A=4 000·1−(1+0,08)−50,08​ = 15 970,84 руб.
2. Фирма предполагает создать специальный фонд в размере 200 тыс.руб., для чего будет вносить в банк 50 тыс.руб. под 15% годовых. Определить срок, необходимый для создания фонда.
   Найдем срок аннуитета: n=ln(SR​·i+1)ln(1+i)​
   n=ln(20050​·0,15+1)ln(1+0,15)​ = 3,363 года

Самостоятельный расчёт аннуитетного платежа

Самый первый из вариантов – произвести расчёт аннуитетных платежей по кредиту на калькуляторе. Тем не менее, разбираться в тонкостях финансовых операций, проводящихся через банк, стоит уметь и самостоятельно. Специалисты банковского дела считают размер аннуитетных ставок по специальной формуле. В результате происходит составление графика, в котором расписывается порядок погашения аннуитета. Формула эта выглядит следующим образом:

Чтобы рассчитать процент по аннуитетному платежу, необходимо остаток по займу умножить на годовой процент, а после разделить результат на 12 (количество месяцев в году). Выглядит это следующим образом:

Чтобы просчитать долю месячного платежа, использующуюся, как сумма погашения основной задолженности (самой суммы кредита, не процентов) в аннуитетной системе, следует от общего займа вычесть проценты:

Конечно, куда проще использовать специальный онлайн-калькулятор аннуитетных платежей по кредиту, чем подсчитывать всё самостоятельно. Однако если вы желаете убедиться в честности банка, стоит научиться рассчитывать аннуитетный платёж самостоятельно. Ещё более рациональным решением будет использовать и аннуитетный калькулятор  на нашем сайте.

Калькуляторы не единственный способ автоматизированного расчета. На любом персональном компьютере есть табличные процессоры со встроенными функциями, подходящими для этой сложной операции. Например, в хорошо знакомой таблице Excel есть функция ПЛТ. С её помощью аннуитетная ставка рассчитывается следующим образом:

• Создаём чистый лист и в любой свободной ячейке задаём соответствующую функцию;
• Вводим необходимые параметры (которые запрашивает программа)

Когда вы закончите ввод, в ячейке увидите интересующую цифру. Простой метод, но не совсем объективный. Ведь есть много нюансов, о которых Excel совсем не спрашивает. Используйте этот метод, если Вы привыкли к данной программе или Вам захотелось испытать “новые возможности”, но в любом-другом случае откажитесь от этого способа.

Плюсы и минусы аннуитетного кредита

Ещё в начале статьи можно сделать вывод, что аннуитетные выплаты подходят не всем. Дело даже не в сложных расчётах,ведь калькуляторы аннуитетных платежей по кредиту, работающие в онлайне, решают эту проблему. Поэтому стоит очертить круг из тех, кому такой заём окажется выгодным.

Преимущества Одинаковая сумма платежа; Ежемесячный платёж ниже; Предоставляется во всех банках; Просто планировать собственные расходы; Процент одобрения выше.

Недостатки Погашаются сначала проценты; Значительные переплаты при ипотеке; Значительные переплаты длительном кредитовании.

Говоря о фактах, кредит, на который действует аннуитетная схема выплат, несколько дороже. В банке Вам всегда посчитают именно аннуитетную ставку, так как она в большей степени выгодна банку. Единственная выгода для заёмщика – это сумма ежемесячного платежа аннуитета, которая значительно ниже до определенного момента.

Как оценить аннуитет

Идея заключается в следующем.

Шаг 1. Сначала рассчитаем приведенную стоимость денежного потока за неограниченный период, начиная с первого же года. Формула, применяемая для этого, элементарна: PV = C / r, где, как мы помним, C – денежный поток, r – ставка дисконтирования.

Шаг 2. Теперь рассчитаем приведенную стоимость бессрочной ренты, приносящей ежегодно денежный поток в размере C, но не с первого года (как на предыдущем шаге), а с года t+1.

Приведенная стоимость такой ренты в год t будет равна значению дроби C / r.

На данный же момент приведенная стоимость интересующего нас денежного потока может быть рассчитана по формуле: PV = C / (r * (1 + r)t).

И та, и другая бессрочные ренты будут приносить денежный поток с года t+1.

Их отличие только в том, что первая бессрочная рента, кроме того, будет генерировать денежный поток еще и в период с 1-го года по t-ый включительно.

Чтобы оценить размер этого денежного потока, нам придется сделать следующий шаг.

Шаг 3. Чтобы определить размер аннуитета, создающего денежный поток в размере C, с первого года по год t, нужно всего лишь найти разницу между двумя описанными выше бессрочными рентами. Приведенная стоимость искомого аннуитета соответственно будет равна разности приведенных стоимостей обеих бессрочных рент:

PV_{аннуитет} = C / r — C / (r * (1 + r)t) = С * [1/r – 1/ (r * (1 + r)t)].

Классификация аннуитета

Аннуитетные платежи весьма разнообразны и делятся на несколько видов, в зависимости от определенных факторов.

Время выплаты стартовых взносов:

• постнумерандо — по окончании первого периода;
• пренумерандо — поступление до начала периода.

Сроки действия:

• срочные платежи;
• пожизненные: передаваемые по наследству, с коррекцией денежных взносов или гарантированные платежи, при которых устанавливается срок выплаты.

Страховые взносы отличаются по характеру выплат и делятся на простые, отложенные, срочные, гарантированные и обладающие защитой личного капитала.

Аннуитеты бывают:

1. фиксированные (равная сумма платежей);
2. валютные (привязанные к валюте, к примеру, к доллару);
3. индексируемые (с коррекцией индекса инфляции);
4. переменные (сумма выплаты привязана к индексу доходности финансового инструмента).

Платежи могут быть ежемесячными, ежеквартальными и ежегодными, и различаться по срочности внесения:

1. срочные, количество выплат фиксировано договором;
2. досрочные;
3. бессрочные;
4. не фиксированные

Классификация зависит и от наименования плательщика:

1. страховые;
2. пенсионные;
3. финансовые (банковские);
4. платежи, производимые юридическими лицами;
5. суммы, вносимые физическими лицами.

Как рассчитать долг на конец месяца в графике аннуитетных платежей

Прежде всего, надо понимать, что именно является вашим долгом по кредиту, и какие выплаты способствуют его уменьшению. В нашем примере вы берёте в кредит 50 000 рублей – это и есть ваш долг. Переплаченные по кредиту проценты (6157 рублей) вашим долгом не являются, это всего лишь вознаграждение банку за предоставленный кредит. Таким образом, можно сделать вывод:

Погашение процентов по кредиту никак не способствует уменьшению вашего долга перед банком.

В кризисные времена банки часто «идут навстречу» своим должникам. Они говорят как-то так: «Мы понимаем, у вас сейчас проблемы! Окей, наш банк готов пойти вам на уступки – можете нам просто погашать проценты, а само тело кредита погашать не надо. Все же люди братья и должны друг другу помогать! Бла-бла-бла…»

На первый взгляд такое предложение может показаться выгодным, а сам банк – «белым и пушистым лапулей». Ага, как бы ни так! Если взять в руки калькулятор и провести простые арифметические расчёты, то сразу становится ясно, что реальное предложение банка выглядит приблизительно так:

«Ребята, вы попали на деньги! Ничего не поделаешь, это жизнь! Предлагаем вам на время (а может и навсегда) стать нашим рабом – будете ежемесячно выплачивать проценты по кредиту, а сам долг погашать не надо (ну, чтобы сумма выплат по процентам не уменьшалась). Ничего личного – это просто бизнес, друзья!»

Теперь запомните главную мысль:

Именно погашение тела кредита вытаскивает вас из долговой ямы. Не процентов, а именно тела кредита.

Наверняка вы уже догадались, как рассчитывается долг на конец месяца в нашем графике платежей. В общем, формула выглядит так:

Обратите внимание! При расчёте долга на конец месяца, от общей суммы текущей задолженности отнимается только та часть платежа, которая идёт на погашение тела кредита (уплаченные проценты сюда не входят). Давайте для наглядности посчитаем, каким будет долг на конец месяца по нашему кредиту после внесения первого платежа:

Давайте для наглядности посчитаем, каким будет долг на конец месяца по нашему кредиту после внесения первого платежа:

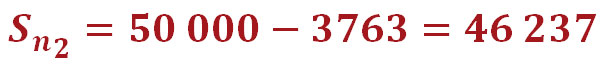
Итак, при первом платеже текущая задолженность по кредиту у нас равна всей сумме займа (50 000 руб.). Чтобы посчитать долг на конец месяца, мы отнимаем от этой суммы не весь ежемесячный платёж (4680 руб.), а только ту часть, которая ушла на погашение тела кредита (3763 руб.). В результате наш долг на конец месяца составит 46 237 руб., именно на эту сумму будут начисляться проценты в следующем месяце. Естественно, они будут меньше, так как сумма долга уменьшилась

Теперь вы понимаете, почему важно погашать именно тело кредита?

Итак, друзья, мы с вами разобрались с формулами и расчетами аннуитетных платежей. Надеемся, теперь у вас нет вопросов по этой теме, и вы запросто сможете произвести все необходимые расчеты, а также составить график аннуитетных платежей по кредиту. Единственное, что бы вам, наверное, хотелось, это как-то автоматизировать процесс расчетов. Вы не поверите, но это возможно! Хотите узнать как? Тогда переходим к публикации: Расчет аннуитетных платежей по кредиту в Excel.

Наши группы:

Почему важно знать, как считается досрочка?

Люди рано или поздно при взаимоотношениях с банком задумываются над вопросом, как банк считает кредиты и вклады? Человеку важно знать, как банк считает кредит, строит график платежей, считает досрочные погашения по кредиту. Данная статья проливает свет на данный вопрос

В ней приводятся формулы и показано как произвести расчет аннуитетного кредита и как рассчитать досрочное погашение займа с аннуитетными платежами.

Допустим вы пытаетесь рассчитать график платежей. Обычно в расчетах таблицы платежей обычно происходит заминка. Особенно интересен график платежей, если делаются досрочные платежи. Знание механизма расчета досрочки позволяет понять, каким образом правильно досрочно погашать, чтоб досрочка была эффективнее всего.

Сам банк за вас не посчитает, а знать сколько будет платеж после досрочного погашения нужно. Ответить на данный вопрос вам поможет финансовый инструмент — кредитный калькулятор с досрочными платежами онлайн.

Расчёт аннуитетного платежа по кредиту

Допустим, вы решили взять в кредит 50 000 рублей на 12 месяцев под 22% годовых. Естественно, тип погашения будет аннуитетный. Вам надо рассчитать сумму ежемесячных взносов по кредиту.

Давайте для начала красиво оформим наши исходные данные (они нам понадобятся не только в этом, но и в дальнейших расчетах):

Сумма кредита: 50 000 руб.Годовая процентная ставка: 22%.Срок кредитования: 12 месяцев.

Итак, прежде чем приступить к расчёту аннуитетного платежа, надо посчитать ежемесячную процентную ставку (в формуле она скрывается под символом i и рассчитывается так: годовая процентная ставка/100/12). В нашем случае получится следующее:

Теперь, когда мы нашли значение i, можно приступать к расчёту размера аннуитетного платежа по нашему кредиту:

Путём несложных математических вычислений выяснилось, что сумма ежемесячных отчислений по нашему кредиту будет равна 4680 рублей.

В принципе, на этом можно было бы закончить нашу статью, но вы же наверняка хотите знать больше. Правда? Вот скажите, вы хотите знать, какую долю в данных выплатах составляют проценты по кредиту, а какую – тело кредита? Да и вообще, сколько вы переплатите по кредиту? Если да, тогда мы продолжаем!

Принципы аннуитета, его преимущества и недостатки

Сформулируем основные принципы формирования аннуитета:

• Проценты, входящие в платеж не зависят от общего срока кредита.
• Проценты, выплачиваемые банку, каждый раз пересчитываются в зависимости от остатка долга и времени фактического пользования кредитом.
• Досрочное погашение кредита не влияет на размер ранее начисленных процентов.
• В регулярный платеж входят проценты за фактическое использование кредита, то есть с даты прошлого платежа до даты текущего платежа. Заемщик оплачивает проценты за прошлый месяц, а не за будущий (не авансом).

Соответственно, мнение, что данный вид платежа выгоден только банку – ошибочно. Проценты начисляются абсолютно честно и каждый месяц уменьшаются. Заемщику же – таким образом намного удобнее планировать свой бюджет, так как сумма его расходов на оплату кредита не меняется весь срок кредитования.

Формула расчета платежа

Существует специальная формула расчета кредита:

При этом:

• Х — ежемесячный аннуитетный платеж;
• S — тело кредита;
• m — процентная ставка банка (ежемесячная), установленная на сумму займа
• N — количество процентных периодов (месяцев).

Зная формулу расчета выплат, очень просто узнать точную сумму аннуитетного платежа. Например: в банке взят кредит на 2 года, в сумме 20 000 руб. Годовая процентная ставка составляет 22%. Как рассчитать ежемесячный взнос?

Месячная процентная ставка вычисляется по формуле m=P/100/12, где Р-годовая процентная ставка финансового учреждения. В данном случае Р=22%, значит

• m = P/100/12 = 22:100:12 = 0,0183;
• S = 20 000;
• N = 24.

Подставив данные в формулы, получаем:

То есть, клиент в течение 2 лет должен каждый месяц платить банку 1037 руб. 20 коп.

Очень просто подсчитать переплату по кредиту: 1 037.20 х 24-20 000 = 4 892.80. Сумма переплаты по кредиту составит 4 892.80 руб.

Калькулятор кредитного платежа, существующий на сайте Сбербанка и других финансовых учреждений, покажет такой же результат. Возможные отличия объясняются округлением полученных сумм или разными процентными ставками.

Дифференцированный кредит03.

Главная особенность такого варианта выплат в том, что к концу кредитного периода сумма взносов значительно уменьшается, то есть, финансовая нагрузка снижается. Рассчитывать размер выплат приходится заново ежемесячно. Рассчитать кредит и аннуитетный, и дифференцированный поможет калькулятор на нашем сайте.

Вернёмся к вопросу дифференцированных платежей. Почему их размер со временем уменьшается? Всё просто: сумму дифференцируют так, чтобы изначально заёмщик выплатил «тело» кредита – основной займ, при этом погашение «тела» осуществляется равными частями. Что касается начисления процентов, то их максимальное количество сосредотачивается как раз на первых взносах, так как насчитываются они на полную сумму кредитования. Далее “тело” займа уменьшается, а вместе с ним уменьшается и процентная надбавка. Для сравнения, в случае, когда взят аннуитетный кредит, размер взносов остаётся фиксированным на всём выплатном периоде.

Подвох в том, что при дифференцированном кредите Вы большую часть ежемесячного платежа отправляете на погашение основной суммы займа, а при аннуитетном на погашение процентов. Возникает вопрос, почему тогда всем не брать дифференцированный кредит?

Примеры дифференцированного кредита04.

Делаем небольшое сравнение на основе реальных примеров и кратких выводов в конце статьи. За основу взяты два вида кредита: потребительский и ипотечное кредитование.

Потребительский кредит:

Сумма кредита 550 000 рублей

• Процентная ставка по кредиту 15,5%
• Период кредитования 36 месяцев или 3 года

Без комиссий и дополнительных платежей

Ипотечное кредитование:

Сумма кредита 2 500 000 рублей

• Процентная ставка по кредиту 15,5%
• Период кредитования 120 месяцев или 10 лет

Без комиссий и дополнительных платежей

Потребительский кредит. Сумма переплаты составит 131 427 рублей. Первый ежемесячный платёж составит 22 381 рублей, второй 22 184 рублей, десятый 20 605 рублей, двадцатый 18 632 рубля. Если бы это был аннуитетный платёж, мы бы равномерно платили каждый месяц 19 200 рублей, но при этом переплата была бы 141 231 рубль. То есть, разница всего ~10 000 рублей? Да, но перейдем ко второму примеру.

Ипотека. Безусловно, ставка по ипотеке 15,5 очень высокая, но не максимальная. Нам знакомы случаи ипотечного кредитования до 18,5% в 2020 году. Это значение не должно Вас пугать, оно взято лишь для примера. Сумма переплаты составит 1 953 645 рублей, первый платёж 53 125 рублей, тридцатый платёж 45 325 рублей, а шестидесятый (спустя 5 лет) 37 248 рублей. Если бы это был аннуитетный платёж, то переплата составила 2 432 316 рублей, что примерно на 500 000 рублей больше, чем при дифференцированном кредите. При этом Вы бы спокойно платили 41 102 рубля каждый месяц.

Выводы. Дифференцированный кредит выгоден лишь при ипотеке и хорошем финансовом благополучии семьи. Данный вид кредита поможет сэкономить при длительном кредитовании, но значительно ослабит Ваш бюджет в первые 40% погашения кредита.

Расчёт процентов по аннуитетным платежам

Посчитать долю процентов в аннуитетных платежах вам поможет вот эта формула:

In

– сумма в аннуитетном платеже, которая идёт на погашение процентов по кредиту;Sn – сумма оставшейся задолженности по кредиту (остаток по кредиту);i – уже знакомая вам ежемесячная процентная ставка (в нашем случае она равна –0.018333 ).

Давайте для наглядности рассчитаем долю процентов в первом платеже по нашему кредиту:

Так как это первый платёж, то суммой оставшейся задолженности по кредиту является весь кредит – 50 000 руб.

Умножив эту сумму на ежемесячную процентную ставку –0.018333 , мы и получим917 руб. – сумму, указанную в нашем графике.

При расчёте суммы процентов в следующем аннуитетном платеже, на месячную процентную ставку умножается долг, который сформировался на конец предыдущего месяца (в нашем случае это 46 237 руб.

). В результате получится848 руб. – размер доли процентов во втором аннуитетном платеже. По такому же принципу рассчитываются проценты в остальных платежах. Далее давайте вычислим составляющую в аннуитетных платежах, которая пойдёт на погашение тела кредита.

Возврат процентов

Как уже говорилось ранее, аннуитетный платеж – это интересный для банка способ погашения долга, так как сначала деньги направляются на погашение процентов, а потом — на тело кредита. Заемщику он будет удобен тем, что в течение всего срока действия договора сумма расходов будет фиксированная. Нюанс заключается в том, что при досрочном погашении долга банк получит больше прибыли в виде процентов. Но заемщик может вернуть часть уплаченной суммы даже в случае рефинансирования. По закону, банк может получить прибыль только за период фактического использования денег клиентом. Поэтому он имеет право требовать часть процентов обратно (ст. 809 ГК РФ).

Клиент в состоянии самостоятельно рассчитать, сколько денег он может вернуть. Для этого нужно вычесть из суммы всех начисленных процентов ту часть, которая приходится на месяцы до реального погашения. Эти данные можно найти в графике платежей, который прилагается к договору. При длительном сроке кредита цифра может быть внушительной.

Пример

По ипотеке на сумму 2 млн рублей, оформленной на 20 лет по ставке 13,75 %, клиент должен заплатить проценты на общую сумму 3,9 млн руб. Если заем был погашен через три года, то возврату подлежит 230 тыс. рублей, то есть четверть уплаченной суммы. Эти данные можно также получить, использовав калькулятор аннуитетных платежей.

Но не все клиенты знают об этом праве. Да и при потребительском кредите сумма излишне уплаченных процентов может составлять несколько сотен рублей. Не каждый захочет выяснять отношения с банком по этому вопросу и портить в дальнейшем себе репутацию.

Выгодно ли платить ипотеку таким способом?

Одним из кредитов, которые оформляют граждане Российской Федерации, является целевой займ, основным назначением которого является покупка недвижимости — ипотека. Будет ли в таком случае выгодна заемщику аннуитетная схема платежа или лучше воспользоваться дифференцированной?

Как советуют специалисты, в том случае, если вы оформляете кредитное обязательство на период, длительность которого менее 10 лет, более выгодным будет дифференцированный платеж. Поскольку ипотечные кредиты, как правило, выдаются на более длительные сроки, то именно аннуитетная схема позволит погашать платежи более удобным способом.

Как рассчитать аннуитетный платеж в Excel

Те, кто читал предыдущую публикацию, наверняка ещё долго будут с ужасом вспоминать формулу аннуитетного платежа. Но сейчас вы, дорогие друзья, можете облегчённо вздохнуть, ибо все расчёты за вас сделает программа Microsoft Excel.

Мы сделаем не просто файлик с одной циферкой. Нет! Мы разработаем настоящий инструмент, с помощью которого вы сможете рассчитать аннуитетный платёж не только для себя, но и для соседа, который ставит свою машину на детской площадке; прыщавого студента, который сутками курит в вашем подъезде; тётки, которая выгуливает свою собаку прямо под вашими окнами – короче, для всех особо одарённых. Кстати, можете поставить где-нибудь возле монитора купюроприёмник и брать с этой публики деньги.

Давайте приступим к разработке нашего кредитного калькулятора. Смотрим на первый рисунок:

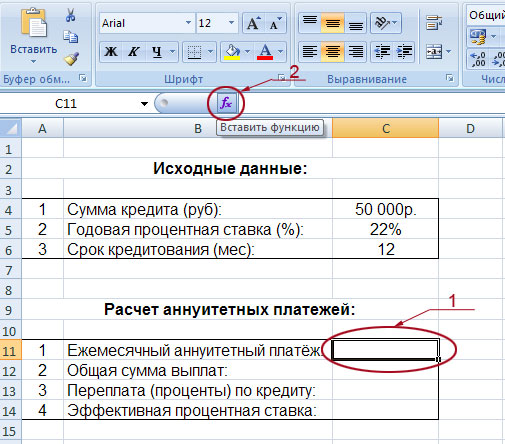
Итак, вы видите два блока. Один с исходными данными, а второй – с расчётами. Исходные данные (сумма кредита, годовая процентная ставка, срок кредитования) вы будете вводить вручную, а во втором блоке будут мгновенно появляться расчёты.

Начнём с расчёта ежемесячной суммы аннуитетного платежа. Для этого надо сделать активным окошко, в котором вы хотите видеть это значение (в нашем случае – это поле C11, на рисунке оно обведено и указано под номером 1). Далее слева от строки формул жмём на «fx» (на рисунке эта кнопка обведена и указана под номером 2). После этих действий у вас появится такая табличка:

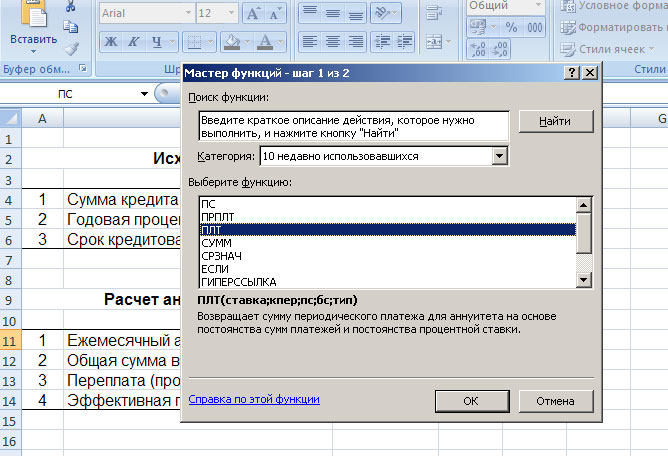
Выбираем функцию «ПЛТ» и жмём «Ок». Перед вами появится таблица, в которую надо будет ввести исходные данные:

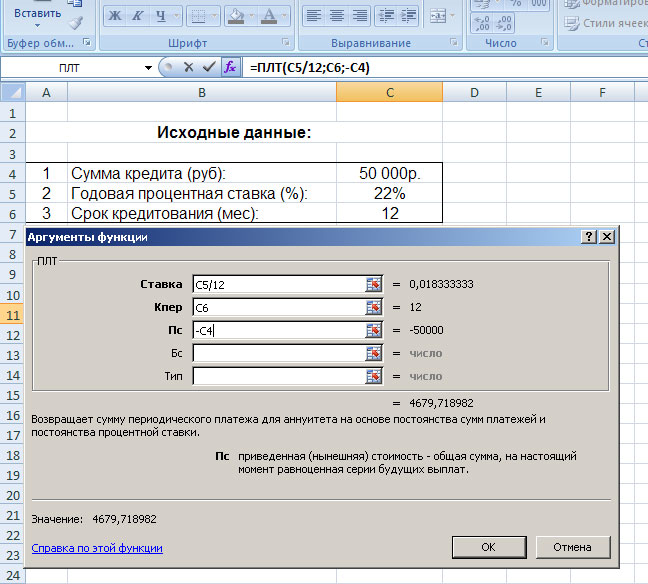
Здесь нам требуется заполнить три поля:

• «Ставка» – годовая процентная ставка по кредиту делённая на 12.
• «Кпер» – общий срок кредитования.
• «Пс» – сумма кредита (указывается со знаком минус).

Обратите внимание на то, что мы не вводим готовые цифры в эту таблицу, а указываем координаты ячеек нашего блока с исходными данными. Так, в поле «Ставка» мы указываем координаты ячейки, в которой будет вписываться вручную процентная ставка (C5) и делим её на 12; в поле «Кпер» указываются координаты ячейки, в которой будет вписываться срок кредитования (C6); в поле «Пс» – координаты ячейки в которой вписывается сумма кредита (C4)

Так как сумма кредита у нас указывается со знаком минус, то перед координатой (C4) мы ставим знак минус.

После того как исходные данные будут введены, жмём кнопку «Ок». В результате мы видим в блоке расчетов точное значение ежемесячного аннуитетного платежа:

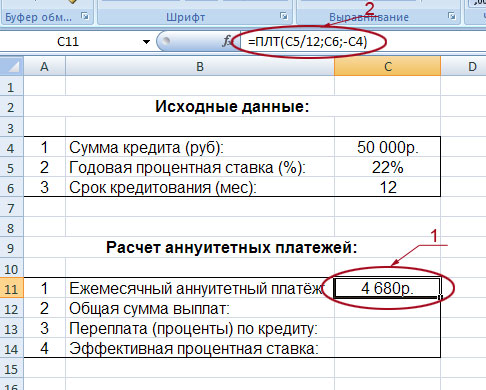
Итак, в данный момент сумма нашего аннуитетного платежа составляет 4680 руб (на рисунке он обведён и указан под номером 1). Если вы будете менять сумму кредита, процентную ставку и общий срок кредитования, то автоматически будет меняться значение вашего аннуитетного платежа.

Кстати, обратите внимание на значение функции, обозначенное на рисунке под номером 2: =ПЛТ(C5/12;C6;-C4). Да, да, это и есть те самые координаты, которые мы вводили в таблицу, выбрав функцию «ПЛТ»

По сути, вы могли бы не проделывать всех тех сложных телодвижений, которые показаны на втором и третьем рисунках. Можно было просто вписать в строке формул то, что там сейчас вписано.

Зная размер аннуитетного платежа несложно посчитать остальные значения нашего расчётного блока:

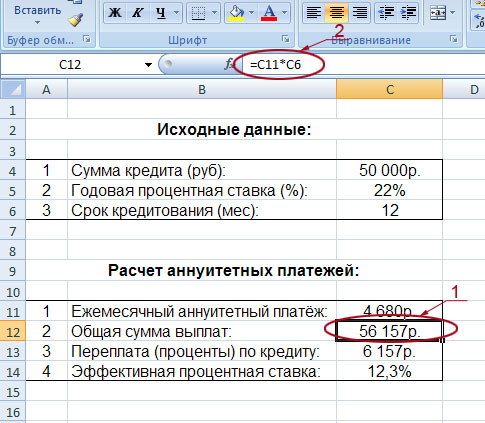
На рисунке наглядно показано, как рассчитана общая сумма выплат (обведена и указана под номером 1). Так как она равна сумме аннуитетного платежа (ячейка C11) умноженной на общее количество месяцев кредитования (ячейка C6), то мы и вписываем в строку формул следующую формулу: =C11*C6 (на рисунке она обведена и указана под номером 2). В результате мы получили значение 56 157 рублей.

Переплата по кредиту рассчитывается ещё проще. От общей суммы выплат (ячейка C12) надо отнять сумму кредита (ячейка C4). В строку вписываем такую формулу: =C12-C4. В нашем примере переплата равна: 6157 рублей.

Ну и последнее значение – эффективная процентная ставка (или полная стоимость кредита). Она рассчитывается так: общую сумму выплат (ячейка C12) делим на сумму кредита (ячейка C4), отнимаем единицу, затем делим всё это на срок кредитования в годах (ячейка C6 делённая на 12). В строке будет такая формула: =(C12/C4-1)/(C6/12). В нашем примере эффективная процентная ставка составляет 12,3%.

Всё! Вот таким нехитрым способом мы с вами составили в программе Microsoft Excel автоматический калькулятор расчета аннуитетных платежей по кредиту, скачать который можно ссылке ниже: